Где собирают Рав 4 для России, Украины, чья сборка как узнать
Одной из популярных в РФ марок автомобилей стала Тойота. Это объясняется признанным японским качеством и высочайшей надёжностью. С 1997-го года в Японии начали массово производить РАВ 4. С того времени кроссовер пережил несколько поколений. И с тех пор производить авто стали рассредоточено на разных предприятиях во многих странах. Где собирают Тойота Рав 4?
В России Rav 4 с 2016 года производят на заводе под Санкт-Петербургом, до этого поставляли из Японии.


Производство Toyota в РФ


Завод Тойота в Санкт-Петербурге
21/12/2007 торжественно открыли завод Тойота в городе Санкт-Петербург, где производят Рав 4 для России.
В церемонии участвовали японские и российские представители власти. В день, когда начали производить авто, цеха посетил также Путин В.В., президент РФ. По состоянию на 2019 год предприятие продолжает производить Тойота РАВ 4 и второй бестселлер марки: Toyota Camry, и в Петербурге организован полный производственный цикл.


Заводы бренда, разбросанные по миру, подчиняются единым стандартам сборки. Для каждой технологической операции разработаны инструкции, выполнение которых постоянно мониторится. Т.е., японское качество встроено в технологию производственного процесса на всех его этапах.
Каждый автомобиль, выходящий с конвейера, подвергается полному контролю качества.
Работники Toyota в Санкт-Петербурге, где собирают Rav4, постоянно учатся у иностранных коллег. На зарубежных тренингах множество российских автомобилестроителей постоянно повышают квалификацию. Каждый работник петербургского предприятия априори вовлечен в оптимизацию производственных операций и повышение качества продукции.


Производственный процесс на заводе Тойота в Шушарах
Развитие завода Тойота в Шушарах:
- 2005 – летом заложили фундамент комбината.
- 2007 – предприятие открыли и начали производить Камри (седан бизнес-класса), в декабре.
- 2010 — начались поставки Камри в Беларусь.
- 2011 — стартовал выпуск К
Где собирается Тойота Рав 4, завод Toyota в России
Из статьи читатель узнает где и в каких странах собирается кроссовер Тойота Рав 4. Чем отличается первая модель от тех, которые выпускаются в последнее время и почему. А также читатель узнает, закроется ли в скором времени проект Тойота Рав 4.
Автовладельцы при покупке машины часто интересуются страной, где она была собрана. Считается, что лучше довериться сборке в европейских странах или азиатских типа Японии или Кореи. Следом можно услышать вопросы о том, где собирают Тойоту Рав 4 для России, есть ли в РФ собственный завод по сборке.
Так где же собирают этот автомобиль. Ответы даны в следующем блоке.
Где происходит сборка Рав 4
Отвечая на вопрос, где собирают Тойота Рав 4, можно дать следующие ответы:
В европейских странах есть заводы по сборке Тойота Рав 4 2019 года в:
- Чехии;
- Великобритании;
- Польше.
Японский производитель Тойота Рав 4 2019 года и прошлых лет установил завод в Южной Америке. А именно в Бразилии.
Однако, не следует думать, что на этих заводах собирается этот автомобиль и для внутреннего рынка Японии. Для жителей своей страны заводы по сборке находятся внутри японских островов. Например, компания Тахара на острове Ацуми занимается производством машин для себя и жителей азиатского рынка.
А вот в Канаде городе Онтарио, завод комплектует машины только для североамериканского континента.
Внимание! На таком заводе, как Тахаока требования по качеству к выпуску машин настолько высоки, что все автомобили, выходящие из него, получают оценку по безопасности в пять звезд на краш-тестах.

Для России
Если раньше автомобили закупали из других стран для продажи на внутреннем рынке России, то сейчас в стране имеется свой собственный завод по сборке и выпуску легендарных Тойота Рав 4.
Этот завод открылся в 2016 году. Владельцы его не стали заморачиваться над названием компании. Поэтому он так и называется «Toyota». Здесь помимо Рав 4 выпускают еще одну модель Тойота Камри.
Предприятие старается учитывать вкус и спрос клиента на те или иные автомобили. Разрабатывает широкий спектр программ по максимизации удобств и комфорта во время поездки на авто, сходящих с конвейера ООО «Toyota». Транспортные средства, которые изготавливаются здесь, выходят сразу адаптированными к климатическим условиям и дорогам.

Характеристики Тойота Рав 4
Где бы ни собирали машину, характеристики остаются напрочь японскими. Отсутствие внимания к мелочам, чего не скажешь, например, о Фольцвагенах немецкого производителя, при сравнивании автомобилей.
Хотя многие автовладельцы подчеркивают эргономичность водительского кресла.
- удобный хват руля;
- хорошо профилированные сиденья;
- большие ходы регулировок.
Все это делает японский кроссовер надежным и удобным, несмотря на невнимание к мелким деталям.
Внимание! По сути изначально автомобиль был представлен как молодежный для активного отдыха. Поэтому его и назвали «Recreation Active Vehicle» (RAV). А цифра 4 означает, что автомобиль полноприводный.
Но чаще всего мало, кто из владельцев этого транспортного средства использует машину для езды по бездорожью. В основном японский транспорт на российских дорогах работает в режиме городского типа.

Плюсы и минусы отечественной сборки
Продолжая отвечать на вопрос, где собирают Тойота Рав 4, следует упомянуть, что качество сборки отечественного оставляет желать лучшего. Вот примеры:
- хромает шумоизоляция. Во время поездок по проселочной дороге, остановке на светофорах, поездках по неровной дороге, слышен шум снаружи авто;
- материал, который используется для обивки сидений используется дешевый. Это не соответствует заявленной стоимости самого транспортного средства.
Пластик может начать скрипеть после одного года пользования автомобилем. А на лакокрасочном покрытии остаются царапины. Это говорит о том, что используется дешевый материал.
Но дело не только в отечественном производителе. Этим грешат и производители других стран, где собирается легендарный автомобиль Тойота Рав 4.

Что будет с Тойота Рав 4
Ходили слухи, что завод в Петербурге прекращает выпуск Тойота Рав 4. Затем эти слухи подтвердили владельцы компании. С октября 2019 года завод переходит на выпуск Рав 4 пятого поколения. А производство автомобиля четвертого поколения будет закрыто.
Это будет обновленный внедорожник, который превзойдет своего предшественника, как говорят производители японского транспорта. Что получит автолюбитель при покупке обновленного Рав 4 пятой генерации:
- новый и брутальный дизайн. Авто будет оснащено новыми видами фар: параболического типа и прожекторного;
- улучшенная управляемость. Будут доработаны проблемы с проходимостью, из-за которых семейное авто прошлых поколений не могло состязаться внедорожниками серии Тойота Ленд Крузер 200;
- сниженный центр тяжести;
- вариаторная коробка передач с механическим редуктором. Теперь автовладелец этой машины сможет вручную управлять первой и задней передачей. Механическая часть улучшает разгон и делает его в десятки раз быстрее, чем автоматическая. А также на внедорожник с вариаторной коробкой и механическим редуктором можно будет не бояться путешествовать по бездорожью в течение длительного времени. Обычные вариаторы быстро выходят из строя, так как предназначены только для городского типа движения;
- полный привод с двумя атмосферными моторами с объемом 2 и 2,5 литров. С первым двигателем автомобиль имеет мощность в 150 лошадиных сил, а со вторым обладает 200 л.с.;
- обновленный пакет безопасности водителя и пассажиров.
Все эти параметры делают новый Тойота Рав 4 лучшим транспортным средством из всех, которые были до этого. Обновленный круиз-контроль, система распознавания дорожных знаков и опознавания пешеходов в ночное время суток, помогает водителю.

Заключение
Первые модификации автомобиля особо не радовали покупателя выдающимися характеристиками. Все-таки эта машина создавалась для надежных, спокойных и семейных поездок на пикники. Поэтому не важно, где собирают транспортное средство Тойота Рав 4 2019 года, многим кажется, что она останется надежной и безопасной, но в плане качества мало что изменится.
Но, если автовладельцу не важен вид, а главное устойчивость на дороге, безопасность семьи на сиденьях пассажиров, хорошая проходимость на грунтовых дорогах, то этот автомобиль будет для него верным другом.
Находим заносчивым кроссовер Toyota RAV4 пятого поколения. Тест-драйв toyota rav4 — ДРАЙВ
- Войти
- Регистрация
- Забыли пароль?
- user
- Выход
- Наши
тест-драйвы - Наши
видео - Цены и
комплектации - Сообщество
DRIVE2
- Новости
- Наши тест-драйвы
- Наши видео
- Поиск по сайту
- Полная версия сайта
- Войти
- Выйти
- Acura
- Alfa Romeo
- Aston Martin
- Audi
- Bentley
- Bilenkin Classic Cars
- BMW
- Brilliance
- Cadillac
- Changan
- Chery
- Chevrolet
- Chrysler
- Citroen
- Daewoo
- Datsun
- Dodge
- Dongfeng
- DS
- FAW
- Ferrari
- FIAT
- Ford
- Foton
- GAC
- Geely
- Genesis
- Great Wall
- Haval
- Hawtai
- Honda
- Hummer
- Hyundai
- Infiniti
- Isuzu
- JAC
- Jaguar
- Jeep
- KIA
- Lada
- Lamborghini
- Land Rover
- Lexus
- Lifan
- Maserati
- Mazda
- Mercedes-Benz
- MINI
- Mitsubishi
- Nissan
- Opel
- Peugeot
- Porsche
- Ravon
- Renault
- Rolls-Royce
- Saab
- SEAT
- Skoda
- Smart
- SsangYong
- Subaru
- Suzuki
- Tesla
- Toyota
- Volkswagen
- Volvo
- Zotye
- УАЗ
- Kunst!
- Тесты шин
- Шпионерия
- Автомобизнес
- Техника
- Наши дороги
- Гостиная
- Автоспорт
- Авторские колонки
- Acura
- Alfa Romeo
- Aston Martin
- Audi
- Bentley
- BCC
- BMW
- Brilliance
- Cadillac
- Changan
- Chery
- Chevrolet
- Chrysler
- Citroen
- Daewoo
- Datsun
- Dodge
- Dongfeng
- DS
- FAW
- Ferrari
- FIAT
- Ford
- Foton
- GAC
- Geely
- Genesis
- Great Wall
- Haima
- Haval
- Hawtai
- Honda
- Hummer
- Hyundai
- Infiniti
- Isuzu
- JAC
- Jaguar
- Jeep
- KIA
- Lada
- Lamborghini
- Land Rover
- Lexus
- Lifan
- Maserati
- Mazda
- Mercedes-Benz
- MINI
- Mitsubishi
- Nissan
- Opel
- Peugeot
- Porsche
- Ravon
- Renault
- Rolls-Royce
- Saab
- SEAT
- Skoda
- Smart
- SsangYong
- Subaru
- Suzuki
- Tesla
- Toyota
- Volkswagen
- Zotye
- УАЗ
ХА! — Авторевю

Мы уже не раз обследовали автомобили Toyota в рубрике «Вторые руки». Серьезные проблемы по части надежности находили редко. И тем ярче на благостной картине блистали слабые сюжеты, которые есть и у кроссоверов Toyota RAV4 серии ХА30 2005—2014 годов выпуска.

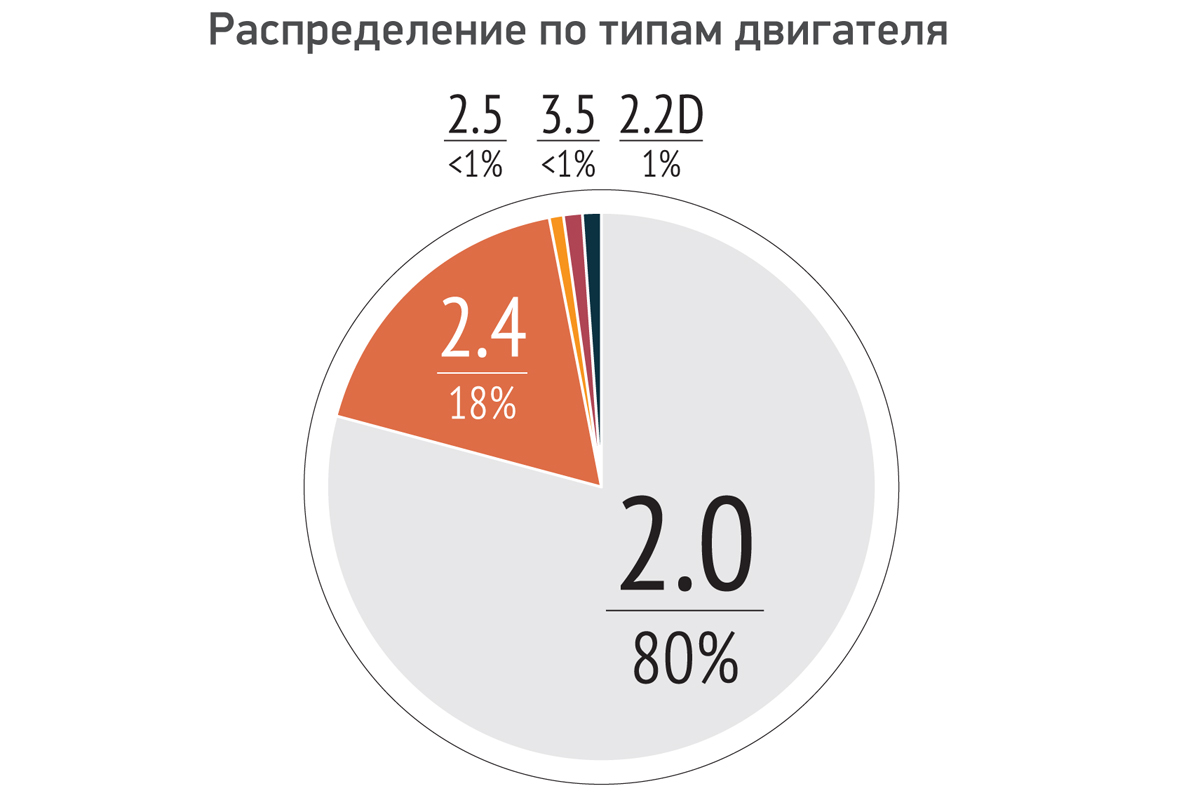
Главное, что вам нужно знать о моторах 2.0 и 2.4 самой популярной серии AZ (60% автомобилей на двоих), — это то, что оба агрегата образца 2000 года с небольшими изменениями (в основном в системе нейтрализации отработавших газов) перекочевали с Рафика предыдущего поколения. А посему имеют неплохие шансы отходить до капремонта не менее 300 тысяч километров. Главное, не экспериментировать с качеством и сроками замены масла. Иначе через 120—150 тысяч километров понадобится досрочная замена не только цепи в приводе ГРМ, но и поршневых колец из-за прогрессирующего масложора. Особенно у очередной раз модернизированных агрегатов моложе 2007 года.

Двигатели серии AZ объемом 2,0 и 2,4 литра различаются диаметром цилиндров (86 мм и 88,5 мм) и ходом поршня (86 мм и 96 мм)
Зато тогда же подлечили самую неприятную болячку, доработав алюминиевый блок цилиндров, — уж больно хлипкой была резьба под крепление ГБЦ. Но и у модернизированных моторов манипуляции с головкой все равно нужно производить крайне осторожно: при срыве резьбы последуют утечка охлаждающей жидкости и перегрев.
И не забывайте, что эти моторы крайне любят чистоту, — а не то придется вести столетнюю войну со снижением холостых оборотов до 500—600 об/мин и последующими вибрациями. В числе противников, помимо загрязнившейся дроссельной заслонки, — клапан холостого хода, форсунки и датчик массового расхода воздуха. Также отложения активно собирает впускной коллектор и его заслонки.
В остальном же после 80—100 тысяч километров нужно приглядывать за водяным насосом (70 долларов) и задним сальником коленвала: они имеют привычку течь. А еще вручную, подбором толкателей, настраивать клапанные зазоры.
У появившейся после рестайлинга 2010 года двухлитровой «четверки» серии 3ZR (38% автомобилей) уже гидрокомпенсаторы. Агрегат образца 2007 года резьбовой слабостью блока не страдал, но усложнение ему на пользу не пошло: помимо механизма изменения подъема клапанов Valvematic, мотор обзавелся системой двойного изменения фаз газораспределения на впускном и выпускном валах (Dual VVT-i) — выход из строя ее муфт (по 200 долларов) нередко случается через 100—120 тысяч километров.

Двухлитровый мотор 3ZR-FAE — самый объемный агрегат в серии ZR
Встречающийся у нас на экс-«американцах» моложе 2008 года мотор 2.5 серии AR считается наиболее удачным. А вот его соотечественник 3.5 серии GR, тоже известный нам по седанам Toyota Camry, хоть и наделяет RAV4 наилучшим темпераментом, но сам капризнее. Во-первых, слабее катушки зажигания. А во-вторых, на экземплярах старше 2008 года нередка течь масла из резиновой части двухсоставной трубки в системе смазки (впоследствии была заменена цельнометаллической).
А вот брать бывших «европейцев» с дизелем 2.2 серии AD не советую: бензиновые моторы удаются Тойоте явно лучше. К маслолюбию и течам помпы и прокладок у AD добавляются дизельные нюансы с необходимостью регулярной очистки клапана рециркуляции отработанных газов (EGR) и выходом из строя форсунок (по 400 долларов) и сажевого фильтра после 200 тысяч километров. Но хуже, что через 150 тысяч километров вокруг гильз могут появиться микротрещины, приводящие к прогару прокладки головки блока и проникновению охлаждающей жидкости в цилиндры.

Японские автопроизводители при рекомендации моторных масел опираются на спецификации Международного комитета по стандартизации и сертификации смазочных материалов (ILSAC). Для бензиновых моторов Тойоты RAV4 третьего поколения рекомендованы масла с одобрением ILSAC GF-4, разработанным в 2004 году. Однако в 2011-м вышел допуск ILSAC GF-5 с более высокими требованиями к энергосбережению, экологичности и защите двигателя, поэтому такой вариант приоритетнее.
Для дизеля с системами EGR или DPF производитель рекомендует малозольные масла уровня ACEA C2, если же данных систем нет — то требования те же, что и для бензиновых двигателей. Рекомендуемая вязкость — 5W-30, а в холодных регионах больше подойдет 0W-20. Срок замены масла не должен превышать 15 тысяч километров, а в тяжелых условиях эксплуатации рекомендуется сократить его вдвое — особенно для дизельных двигателей, если нет возможности постоянно заправлять автомобиль качественным топливом уровня Euro 5.
В «автомат» залита жидкость уровня свойств Toyota WS. Предписан контроль каждые 60 тысяч километров, но для увеличения срока службы коробки с такой же периодичностью лучше производить замену.
В «механике» масло уровня API GL-4 75W-90 также необходимо менять с периодичностью 60 тысяч километров. А вот у вариатора период замены в полтора раза больше — 90 тысяч километров (трансмиссионное масло — класса Toyota CVT TC).
Первая замена долгоиграющей карбоксилатной (OAT) охлаждающей жидкости необходима при достижении пробега 150 тысяч километров, далее — каждые 90 тысяч. И не забывайте для собственной безопасности раз в 30 тысяч километров обновлять тормозную жидкость. Причем вместо рекомендованной, но устаревшей DOT 3 советую применять лучшую по характеристикам DOT 4.

Для бензиновых и дизельных двигателей: масло G-Energy Far East 5W-30/0W-20
Для дизельных двигателей с EGR/DPF: масло G-Energy F Synth C2/C3 5W-30
Для АКП: масло G-Box ATF DX VI
Для МКП: масло G-Box GL-4/GL-5 75W-90
Для вариатора: масло G-Box CVT
Для системы охлаждения: жидкость G-Energy Antifreeze SNF 40
Для тормозной системы: жидкость G-Energy Expert DOT 4
| Таблица двигателей автомобилей Toyota RAV4 (XA30) | |||||
|---|---|---|---|---|---|
| Серия | Рабочий объем, см³ | Мощность, л.с./кВт/об/мин | Обозначение | Годы выпуска | Особенности |
| Бензиновые | |||||
| 1AZ-FE | 1998 | 152/112/6000 | FE | 2006—2010 | R4, DOHC, 16 клапанов |
| 2AZ-FE | 2362 | 170/125/6000 | FE | 2006—2013 | R4, DOHC, 16 клапанов |
| 3ZR-FAE | 1986 | 148/109/6100 | FE | 2008—2013 | R4, DOHC, 16 клапанов |
| 3ZR-FAE | 1986 | 158/116/6200 | FE | 2008—2013 | R4, DOHC, 16 клапанов |
| 2AR-FE | 2494 | 182/133/6000 | FE | 2008—2012 | R4, DOHC, 16 клапанов |
| 2GR-FE | 3458 | 269/197/6200 | FE | 2005—2013 | V6, DOHC, 24 клапана |
| 2GR-FE | 3458 | 273/201/6200 | FE | 2005—2013 | V6, DOHC, 24 клапана |
| Дизельные | |||||
| 1AD-FНV | 1998 | 116/85/3800 | common rail | 2005—2006 | R4, DOHC, 16 клапанов, турбонаддув |
| 2AD-FНV | 2231 | 136/100/3600 | common rail | 2006—2013 | R4, DOHC, 16 клапанов, турбонаддув |
| 2AD-FНV | 2231 | 150/110/3600 | common rail | 2010—2013 | R4, DOHC, 16 клапанов, турбонаддув |
| 2AD-FНV | 2231 | 177/130/3600 | common rail | 2006—2013 | R4, DOHC, 16 клапанов, турбонаддув |
| Электрический | 154/113 | 2012—2014 | |||
| FE — распределенный впрыск; common rail — аккумуляторная система впрыска; R4 — рядный четырехцилиндровый двигатель; V6 — V-образный шестицилиндровый двигатель; DOHC — два распредвала в головке блока цилиндров | |||||
«Автомат» или вариатор?
Вот в неумении делать надежные механические коробки передач Тойоту упрекнуть трудно, и агрегаты на RAV4 (16% автомобилей) не исключение. Если не таскать прицеп с бревнами, то и у пятиступки, и у появившейся после рестайлинга шестиступенчатой коробки даже сцепление способно продержаться до рекордных 180—200 тысяч километров.Полная версия доступна только подписчикамПодпишитесь прямо сейчас
я уже подписанГрафическое изображение линейных неравенств
Это график линейного неравенства:
Неравенство y ≤ x + 2
Вы можете увидеть линию y = x + 2, а заштрихованная область — это место, где y меньше или равно x + 2
Линейное неравенство
Линейное неравенство похоже на линейное уравнение (например, y = 2x + 1 ) …
… но у него будет неравенство типа <,>, ≤ или ≥ вместо = .
Как построить график линейного неравенства
Сначала нарисуйте линию «равно», затем заштрихуйте нужную область.
Есть три шага:
- Измените уравнение так, чтобы «y» находилось слева, а все остальное — справа.
- Постройте линию « y = » (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y < или y> )
- Затенение над линией для «больше чем» ( y> или y≥ )
или ниже линии для «меньше чем» ( y < или y≤ ).
Давайте попробуем несколько примеров:
Пример: y≤2x-1
1. Неравенство уже имеет «y» слева и все остальное справа, поэтому нет необходимости переставлять
2. График y = 2x-1 (сплошная линия, потому что y≤ включает , равное )
3. Закрасьте область ниже (поскольку y на меньше или равно)
Пример: 2y — x ≤ 6
1.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Начать с: 2y — x ≤ 6
Добавьте x к обеим сторонам: 2y ≤ x + 6
Разделить все на 2: y ≤ x / 2 + 3
2. Теперь постройте y = x / 2 + 3 (сплошная линия, потому что y≤ включает , равное )
3. Закрасьте область ниже (поскольку y на меньше или равно)
Пример: y / 2 + 2> x
1.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Начать с: y / 2 + 2> x
Вычтем 2 с обеих сторон: y / 2> x — 2
Умножить все на 2: y> 2x — 4
2. Теперь постройте y = 2x — 4 (пунктирная линия, потому что y> не включает в себя равно)
3. Заштрихуйте область сверху (поскольку y на больше )
Пунктирная линия показывает, что неравенство не включает линию y = 2x-4 .
Два особых случая
У вас также может быть горизонтальная или вертикальная линия:
| Здесь показано, где y меньше 4 (от линии y = 4 вниз, но не включая ее) Обратите внимание, что у нас есть пунктирная линия, чтобы показать, что она не включает где y = 4 | В этом даже нет y! Он имеет линию x = 1 и закрашен для всех значений x, превышающих (или равных) 1 |
Квадратные уравнения
Пример квадратного уравнения :
Квадратные уравнения образуют красивые кривые, такие как эта:
Имя
Название Quadratic происходит от «quad», что означает квадрат, потому что переменная возводится в квадрат (например, x 2 ).
Его также называют «уравнением степени 2» (из-за «2» на x )
Стандартная форма
Стандартная форма квадратного уравнения выглядит так:
- a , b и c — известные значения. a не может быть 0.
- « x » — это переменная или неизвестно (мы еще этого не знаем).
Вот несколько примеров:
| 2x 2 + 5x + 3 = 0 | В этом a = 2 , b = 5 и c = 3 | |
| x 2 — 3x = 0 | Это немного сложнее:
| |
| 5x — 3 = 0 | Ой! Это , а не квадратное уравнение: оно отсутствует x 2 (другими словами a = 0 , что означает, что оно не может быть квадратичным) |
Поиграйте с ним
Поиграйте с «Проводником квадратного уравнения», чтобы увидеть:
- график, а
- решений (называемых «корнями»).
Скрытые квадратные уравнения!
Как мы видели ранее, Стандартная форма квадратного уравнения — это
Но иногда квадратное уравнение так не выглядит!
Например:
| Скрытый | в стандартной форме | a, b и c | |
|---|---|---|---|
| x 2 = 3x — 1 | Переместить все термины в левую часть | x 2 — 3x + 1 = 0 | a = 1, b = −3, c = 1 |
| 2 (w 2 — 2w) = 5 | Развернуть (снять скобки), и переместите 5 влево | 2 Вт 2 — 4 Вт — 5 = 0 | a = 2, b = −4, c = −5 |
| z (z − 1) = 3 | Разверните и переместите 3 влево | z 2 — z — 3 = 0 | а = 1, b = -1, с = -3 |
Как их решить?
В « решениях » квадратного уравнения равно нулю .
Их также называют « корней », или иногда « нулей »
Обычно существует 2 решения (как показано на этом графике).
И есть несколько разных способов найти решения:
Или мы можем использовать специальную квадратичную формулу :Просто введите значения a, b и c и выполняйте вычисления.
Сейчас мы рассмотрим этот метод более подробно.
О квадратичной формуле
Плюс / Минус
Прежде всего, что это за плюс / минус, который выглядит как ±?
± означает, что есть ДВА ответа:
x = −b + √ (b 2 — 4ac) 2a
x = −b — √ (b 2 — 4ac) 2a
Вот пример с двумя ответами:
Но не всегда так получается!
- Представьте, что кривая «просто касается» оси x.
- Или представьте, что кривая настолько высока , что даже не пересекает ось x!
Вот тут-то нам и помогает «Дискриминант» …
Дискриминант
Вы видите b 2 — 4ac в приведенной выше формуле? Он называется Дискриминант , потому что он может «различать» возможные типы ответов:
- когда b 2 — 4ac положительный, мы получаем два Реальных решения
- , когда он равен нулю, мы получаем только ОДНО реальное решение (оба ответа одинаковы)
- при отрицательном значении получаем пару Комплексных решений
Комплексные решения? Давайте поговорим о них после того, как мы увидим, как использовать формулу.
Использование квадратичной формулы
Просто введите значения a, b и c в квадратную формулу и выполните вычисления.
Пример: Решить 5x 2 + 6x + 1 = 0
Коэффициенты: a = 5, b = 6, c = 1
Квадратичная формула: x = −b ± √ (b 2 — 4ac) 2a
Вставьте a, b и c: x = −6 ± √ (6 2 — 4 × 5 × 1) 2 × 5
Решить: x = −6 ± √ (36 -20) 10
х = −6 ± √ (16) 10
х = −6 ± 4 10
х = -0.2 или −1
Ответ: x = −0,2 или x = −1
И мы их видим на этом графике.
| Чек -0,2 : | 5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1 = 5 × (0,04) + 6 × (-0,2) + 1 = 0,2 — 1,2 + 1 = 0 | |
| Чек -1 : | 5 × ( −1 ) 2 + 6 × ( −1 ) + 1 = 5 × (1) + 6 × (-1) + 1 = 5–6 + 1 = 0 |
Вспоминая формулу
Добрый читатель предложил спеть это к «Pop Goes the Weasel»:
| ♫ | «x равно минус b | ♫ | «Вокруг тутового куста | |
| плюс или минус квадратный корень | Обезьяна погналась за лаской | |||
| квадрата b минус четыре a c | Обезьяна думала, что все было весело | |||
| ВСЕ более двух а « | Поп! идет ласка » |
Попробуйте спеть его несколько раз, и он застрянет у вас в голове!
Или вы можете вспомнить эту историю:
х = −b ± √ (b 2 — 4ac) 2a
«Негативный мальчик думал, да или нет, о том, чтобы пойти на вечеринку,
на вечеринке он разговаривал с квадратным мальчиком, но не с четырьмя классными цыпочками.
В 2 часа ночи все закончилось. «
Комплексные решения?
Когда Дискриминант (значение b 2 — 4ac ) отрицательный, мы получаем пару Комплексных решений … что это означает?
Это означает, что наш ответ будет включать в себя мнимые числа. Вау!
Пример: Решить 5x 2 + 2x + 1 = 0
Коэффициенты равны : a = 5, b = 2, c = 1
Обратите внимание, что дискриминант отрицательный: b 2 — 4ac = 2 2 — 4 × 5 × 1
= −16
Используйте квадратичную формулу : x = −2 ± √ (−16) 10
√ (-16) = 4 i
(где i — мнимое число √ − 1)
Итак: x = −2 ± 4 и 10
Ответ: x = −0.2 ± 0,4 и
График не пересекает ось абсцисс. Вот почему мы получили комплексные числа.
В некотором смысле это проще: нам не нужно больше вычислений, просто оставьте -0,2 ± 0,4 i .
Пример: Решить x 2 — 4x + 6,25 = 0
Коэффициенты равны : a = 1, b = −4, c = 6,25
Обратите внимание, что дискриминант отрицательный: b 2 — 4ac = (−4) 2 — 4 × 1 × 6.25
= −9
Используйте квадратичную формулу : x = — (- 4) ± √ (−9) 2
√ (−9) = 3 i
(где i — мнимое число √ − 1)
Итак: x = 4 ± 3 i 2
Ответ: x = 2 ± 1,5 i
График не пересекает ось абсцисс.Вот почему мы получили комплексные числа.
НО перевернутое зеркальное отображение нашего уравнения действительно пересекает ось x в 2 ± 1,5 (примечание: отсутствует i ).
Просто интересный факт для вас!
Сводка
- Квадратное уравнение в стандартной форме: ax 2 + bx + c = 0
- Квадратичные уравнения могут быть разложены на множители
- Квадратичная формула: x = −b ± √ (b 2 — 4ac) 2a
- Когда дискриминант ( b 2 −4ac ) равен:
- положительный, есть 2 реальных решения
- ноль, есть одно реальное решение
- негатив, есть 2 комплексных решения
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
Введите полиномиальное неравенство вместе с переменной, для которой необходимо решить, и нажмите кнопку «Решить».
В главе 2 мы установили правила решения уравнений с использованием чисел в арифметике. Теперь, когда мы изучили операции с числами со знаком, мы будем использовать те же правила для решения уравнений, содержащих отрицательные числа. Мы также изучим методы решения и построения графиков неравенств с одним неизвестным.
РЕШЕНИЕ УРАВНЕНИЙ НА ЗАПИСАННЫХ ЧИСЛАХ
ЗАДАЧИ
По завершении этого раздела вы сможете решать уравнения, содержащие числа со знаком.
Пример 1 Решите относительно x и проверьте: x + 5 = 3
Решение
Используя те же процедуры, что и в главе 2, мы вычитаем 5 из каждой части уравнения, получая
Пример 2 Решите относительно x и проверьте: — 3x = 12
Решение
Разделив каждую сторону на -3, получаем
| Всегда проверяйте исходное уравнение. |
| Другой способ решения уравнения 3x — 4 = 7x + 8 — сначала вычесть 3x из обеих сторон, получив -4 = 4x + 8, , затем вычесть 8 с обеих сторон и получить -12 = 4x . Теперь разделите обе стороны на 4, получив — 3 = x или x = — 3. |
| Сначала удалите круглые скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите буквальное уравнение.
- Примените ранее изученные правила для решения буквальных уравнений.
Уравнение, содержащее более одной буквы, иногда называют буквальным уравнением . Иногда бывает необходимо решить такое уравнение для одной из букв через другие. Пошаговая процедура, описанная и использованная в главе 2, остается действительной после удаления любых символов группировки.
Пример 1 Решить относительно c: 3 (x + c) — 4y = 2x — 5c
Решение
Сначала удалите круглые скобки.
Здесь мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все другие члены с другой стороны уравнения. Таким образом, получаем
| Помните, что abx — это то же самое, что 1abx. Делим на коэффициент при x, который в данном случае равен ab. |
| Решите уравнение 2x + 2y — 9x + 9a, сначала вычтя 2v из обеих частей. Сравните полученное решение с полученным в примере. |
Иногда форму ответа можно изменить. В этом примере мы могли бы умножить числитель и знаменатель ответа на (- l) (это не меняет значения ответа) и получить
Преимущество этого последнего выражения перед первым в том, что в ответе не так много отрицательных знаков.
| Умножение числителя и знаменателя дроби на одно и то же число является использованием фундаментального принципа дробей. |
Наиболее часто используемые буквальные выражения — это формулы из геометрии, физики, бизнеса, электроники и т. Д.
Пример 4 — это формула для площади трапеции. Решите для c.
| Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями. Удаление скобок не означает их просто стереть. Мы должны умножить каждый член в круглых скобках на коэффициент, стоящий перед скобками. Изменять форму ответа не обязательно, но вы должны уметь распознать правильный ответ, даже если форма не та. |
Пример 5 — это формула, дающая проценты (I), полученные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда известны сумма процентов, основная сумма и количество дней.
Решение
Задача требует решения для р.
Обратите внимание, что в этом примере r оставлено с правой стороны, и поэтому вычисление было проще. При желании мы можем переписать ответ по-другому.
ГРАФИЧЕСКИЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Используйте символ неравенства для обозначения относительного положения двух чисел на числовой прямой.
- График неравенств на числовой прямой.
Мы уже обсуждали набор рациональных чисел как числа, которые могут быть выражены как отношение двух целых чисел.Существует также набор чисел, называемых иррациональными числами , , которые нельзя выразить как отношение целых чисел. В этот набор входят такие числа как и так далее. Набор, состоящий из рациональных и иррациональных чисел, называется действительными числами.
Для любых двух действительных чисел a и b всегда можно заявить, что Часто нас интересует только то, равны ли два числа или нет, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равны. равный.
Символы представляют собой символы неравенства или отношения порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем символ как «больше чем». Например, a> b читается как «a больше, чем b». Обратите внимание: мы заявили, что обычно читаем
а
| Какое положительное число можно добавить к 2, чтобы получить 5? |
Проще говоря, это определение утверждает, что a меньше b, если мы должны что-то добавить к a, чтобы получить b.Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой прямой, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой прямой. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3
| Мы также можем написать 6> 3. |
Пример 2 — 4
| Мы также можем написать 0> — 4. |
Пример 3 4> — 2, потому что 4 находится справа от -2 в числовой строке.
Пример 4 — 6
Математическое утверждение x
| Понимаете, почему невозможно найти наибольшее число меньше 3? |
На самом деле назвать число x, которое является наибольшим числом меньше 3, — задача невыполнимая. Однако это может быть указано в числовой строке.Для этого нам нужен символ, обозначающий значение такого оператора, как x
Символы (и), используемые в числовой строке, указывают на то, что конечная точка не включена в набор.
Пример 5 График x
Решение
Обратите внимание, что на графике есть стрелка, указывающая на то, что линия продолжается без конца влево.
| На этом графике представлено каждое действительное число меньше 3. |
Пример 6 График x> 4 на числовой прямой.
Решение
| На этом графике представлено каждое действительное число больше 4. |
Пример 7 График x> -5 на числовой прямой.
Решение
| На этом графике представлены все действительные числа больше -5. |
Пример 8 Постройте числовой график, показывающий, что x> — 1 и x
Решение
Выписка x> — 1 и x
| На этом графике представлены все действительные числа от -1 до 5. |
Пример 9 График — 3
Решение
Если мы хотим включить конечную точку в набор, мы используем другой символ:. Мы читаем эти символы как «равно или меньше» и «равно или больше».
Пример 10 x>; 4 указывает число 4 и все действительные числа справа от 4 в числовой строке.
Символы [и] в числовой строке указывают, что конечная точка включена в набор.
| Вы обнаружите, что такое использование круглых и квадратных скобок согласуется с их использованием в будущих курсах математики. |
| На этом графике представлены число 1 и все действительные числа больше 1. |
| На этом графике представлено число 1 и все действительные числа, меньшие или равные — 3. |
Пример 13 Напишите алгебраическое утверждение, представленное следующим графиком.
Пример 14 Напишите алгебраическое выражение для следующего графика.
| На этом графике представлены все действительные числа от -4 до 5 , включая от -4 до 5. |
Пример 15 Напишите алгебраическое выражение для следующего графика.
| Этот график включает 4, но не -2. |
Пример 16 График на числовой прямой.
Решение
В этом примере возникает небольшая проблема. Как мы можем указать на числовой строке? Если мы оценим суть дела, то другой человек может неправильно истолковать это утверждение. Не могли бы вы сказать, представляет ли эта точка или может быть? Поскольку цель графика — прояснить, всегда обозначает конечную точку .
| График используется для передачи утверждения. Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, если быть точным. |
УСТРАНЕНИЕ НЕРАВЕНСТВ
ЗАДАЧИ
По завершении этого раздела вы сможете решить неравенства с одним неизвестным.
Решение неравенств обычно включает те же основные правила, что и уравнения. Есть одно исключение, которое мы скоро обнаружим. Однако первое правило аналогично тому, что используется при решении уравнений.
Если к каждой стороне неравенства добавлено одинаковое количество, результаты будут неравными в том же порядке.
Пример 1 Если 5
Пример 2 Если 7
Мы можем использовать это правило для решения некоторых неравенств.
Пример 3 Решить относительно x: x + 6
Решение
Если мы прибавим -6 к каждой стороне, мы получим
Изобразив это решение на числовой прямой, получим
| Обратите внимание, что процедура такая же, как и при решении уравнений. |
Теперь мы воспользуемся правилом сложения, чтобы проиллюстрировать важную концепцию, касающуюся умножения или деления неравенств.
Предположим, что x> a.
Теперь добавьте — x к обеим сторонам по правилу сложения.
| Помните, добавление одинаковой величины к обеим сторонам неравенства не меняет его направления. |
Теперь добавьте -a с обеих сторон.
Последний оператор — a> -x можно переписать как — x <-a. Поэтому мы можем сказать: «Если x> a, то — x
Если неравенство умножается или делится на отрицательное число , результаты будут неравными в порядке , противоположном .
| Например: Если 5> 3, то -5 |
Пример 5 Решите относительно x и изобразите решение: -2x> 6
Решение
Чтобы получить x в левой части, мы должны разделить каждый член на — 2. Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.
| Обратите внимание: как только мы делим на отрицательную величину, мы должны изменить направление неравенства. |
Обратите особое внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменять направление символа неравенства. Это единственное различие между решением уравнений и решением неравенств.
| Когда мы умножаем или делим на положительное число, изменений нет. Когда мы умножаем или делим на отрицательное число, направление неравенства меняется. Будьте осторожны — это источник многих ошибок. |
После того, как мы удалили круглые скобки и остались только отдельные члены в выражении, процедура поиска решения почти такая же, как в главе 2.
Давайте теперь рассмотрим пошаговый метод из главы 2 и отметим разницу при решении неравенств.
Первый Исключите дроби, умножив все члены на наименьший общий знаменатель всех дробей. (Без изменений, когда мы умножаем на положительное число.)
Второй Упростите, объединив одинаковые члены с каждой стороны неравенства. (Без изменений)
Третий Сложите или вычтите количества, чтобы получить неизвестное с одной стороны и числа с другой.(Без изменений)
Четвертый Разделите каждый член неравенства на коэффициент неизвестной. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет отменено. (Это важное различие между уравнениями и неравенствами.)
| Единственное возможное отличие заключается в последнем шаге. |
| Что нужно делать при делении на отрицательное число? |
| Не забудьте пометить конечную точку. |
РЕЗЮМЕ
Ключевые слова
- Литеральное уравнение — это уравнение, состоящее из более чем одной буквы.
- Символы представляют собой символы неравенства или отношения порядка .
- a a находится слева от b в строке действительных чисел.
- Двойные символы: указывают, что конечные точки включены в набор решений .
Процедуры
- Чтобы решить буквальное уравнение для одной буквы через другие, выполните те же действия, что и в главе 2.
- Чтобы решить неравенство, используйте следующие шаги:
Шаг 1 Исключите дроби, умножив все члены на наименьший общий знаменатель всех дробей.
Шаг 2 Упростите, объединив одинаковые термины с каждой стороны неравенства.
Шаг 3 Сложите или вычтите количества, чтобы получить неизвестное с одной стороны и числа с другой.
Шаг 4 Разделите каждый член неравенства на коэффициент неизвестной. Если коэффициент положительный, неравенство останется прежним.Если коэффициент отрицательный, неравенство будет отменено.
Шаг 5 Проверьте свой ответ.
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
Введите уравнение вместе с переменной, для которой вы хотите его решить, и нажмите кнопку «Решить».
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найдите число, которое при добавлении к 3 дает 7»
можно записать как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x обозначают число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как предложения слов могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, совпадает ли левый член с правым.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 — решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.
Пример 2 Найдите решение каждого уравнения путем осмотра.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИСЛЕНИЯ
В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам необходимы некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
эквивалентны уравнениям, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.
Если одинаковое количество прибавляется или вычитается из обоих элементов уравнения, полученное уравнение эквивалентно исходному уравнение.
в символах,
a — b, a + c = b + c и a — c = b — c
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 из каждого члена.
Решение Если вычесть 3 из каждого члена, получим
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
, объединив одинаковые термины, а затем добавив по 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решите 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим
2x + 1- 1 = x — 2-1
2x = х — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2х-х = х — 3 — х
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
, где переменная имеет отрицательный коэффициент.Хотя при осмотре можно увидеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. При желании мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА DIVISION
Рассмотрим уравнение
3x = 12
Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.
в символах,
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Разделив оба элемента на -4, получим
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые термины, чтобы получить
5лет = 20
Тогда, разделив каждый член на 5, получим
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
РешениеСначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединяя одинаковые термины, получаем
3x = -9
Наконец, мы разделим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
в символах,
a = b и a · c = b · c (c ≠ 0)
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
путем умножения каждого члена на 6.
Решение Умножение каждого члена на 6 дает
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.
Пример 2 Решить
Решение Сначала умножьте каждый член на 5, чтобы получить
Теперь разделите каждого члена на 3,
Пример 3 Решить.
Решение Во-первых, упростите над дробной чертой, чтобы получить
Затем умножьте каждый член на 3, чтобы получить
Наконец, разделив каждого члена на 5, получим
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.
Шаги по решению уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы разделим каждый член на 7, чтобы получить
В следующем примере мы упрощаем над полосой дроби перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Во-первых, мы объединяем одинаковые термины, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы делим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую одну из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.
Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть
d = rt
(24) = (3) т
8 = т
Часто бывает необходимо решить формулы или уравнения, в которых существует более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
из которых по закону симметрии
В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить
, затем разделив каждый член на a, мы получим
.