что это, на что влияет, как измеряется :: Autonews
www.adv.rbc.ru
www.adv.rbc.ru
www.adv.rbc.ru
Autonews
Телеканал
Газета
Pro
Инвестиции
+
Новая экономика
Тренды
Недвижимость
Спорт
Стиль
Национальные проекты
Город
Крипто
Исследования
Кредитные рейтинги
Франшизы
Конференции
Спецпроекты СПб
Конференции СПб
Спецпроекты
Проверка контрагентов
Библиотека
Подкасты
ESG-индекс
Политика
Экономика
Бизнес
Технологии и медиа
Финансы
РБК КомпанииРБК Life
www.
Фото: Shutterstock
www.adv.rbc.ru
Читайте также
От вылета диска напрямую зависят безопасность, управляемость и срок службы некоторых компонентов автомобиля.
- Что такое
- На что влияет
- Как измеряется
- Таблица вылета
- Как подобрать
www.adv.rbc.ru
Эксперт в этом материале: Вячеслав Субботин, директор гоночной команды «ГАЗ Рейд Спорт» и автор программы «Минтранс» на телеканале РЕН ТВ
Что такое вылет диска
Вылет диска — это расстояние между привалочной плоскостью и осевой линией колесного диска, то есть воображаемой серединой колеса. Данный показатель в обязательном порядке указывается на каждом диске, вне зависимости от того, к какому типу относится изделие (кованый, литой, штампованный). Маркировка наносится непосредственно на обод штампованных дисков и на привалочную плоскость (либо спицы литых и кованых дисков).
Понять, что перед вами параметр вылета, можно по маркировке ЕТ/OFFSET (einpresstiefe — глубина вставки). Цифровое значение указывается в миллиметрах. К примеру, если на ободе указан параметр ЕТ42, это означает, что диск имеет положительный вылет в 42 миллиметра.
Величина вылета колесных дисков варьируется в широких пределах — от нулевой, когда привалочная плоскость находится непосредственно в центре колеса, до сильно положительной или отрицательной (при отрицательном значении вылета в маркировке ставится значок «-»). Этот параметр задается производителем транспортного средства в зависимости от конкретных технических особенностей.
Стандартный, «заводской» вылет обеспечивает оптимальную работу ступичных подшипников и элементов подвески. Кроме того, диск с правильным вылетом не выпирает из колесной арки и не заходит в нее слишком глубоко, он не цепляется за тормозной суппорт.
Если с нулевым вылетом вопросов у автомобилистов обычно не возникает, то с положительным и отрицательным все обстоит немного иначе. Понять, с каким именно вылетом вы имеете дело, довольно просто даже визуально. При положительном значении ET плоскость, контактирующая со ступицей, находится перед осевой линией диска (площадка смещена к внешней стороне, диск глубже заходит внутрь арки), а при отрицательном — за ней (площадка смещена к внутренней стороне, диск выпирает наружу). Чем вылет меньше по сравнению со штатным, «заводским», тем больше колеса будут выпирать наружу и тем шире будет колея.
Понять, с каким именно вылетом вы имеете дело, довольно просто даже визуально. При положительном значении ET плоскость, контактирующая со ступицей, находится перед осевой линией диска (площадка смещена к внешней стороне, диск глубже заходит внутрь арки), а при отрицательном — за ней (площадка смещена к внутренней стороне, диск выпирает наружу). Чем вылет меньше по сравнению со штатным, «заводским», тем больше колеса будут выпирать наружу и тем шире будет колея.
На что влияет вылет диска
В магазине можно подобрать комплект дисков, подходящих по числу крепежных отверстий и расстоянию между ними, но при этом параметр вылета может отличаться от заданного производителем. Продавцам важно реализовать свой товар: если колесо нормально крепится и не цепляет детали подвески, то по их мнению, никаких проблем не возникнет. В действительности это далеко не так. К примеру, официальные дилеры, обнаружив «неправильные» диски, могут просто отказать в гарантийном ремонте. Сейчас объясним, почему.
Величину вылета оригинальных колесных дисков определяют конструкторы автомобиля на этапе проектирования. Геометрия колеса подбирается под множество параметров: предполагаемую нагрузку, скоростные характеристики, элементы подвески, тормозной системы и множество других нюансов. Именно по этой причине конкретная величина ET указывается в инструкции по эксплуатации. Нередко у дисков каждого из рекомендуемых диаметров свой вылет. Прислушиваться стоит только к рекомендациям автопроизводителя, но никак не к советам менеджера магазина автозапчастей.
Подбирая ЕТ, конструкторы ориентируются на модель распределения векторов сил в подвеске. Пятно контакта шины с дорогой — это точка приложения данных сил. Именно сквозь его центр должна проходить средняя линия колеса. В эту же область попадает вектор силы стойки подвески. При отклонении вылета от нормального значения возникает смещение средней линии и оси подвески, что, в свою очередь, приводит к ухудшению управляемости, ускоренному износу элементов подвески и компонентов рулевого управления.
Фото: Shutterstock
Основные последствия неправильного вылета:
- Ухудшение управляемости и снижение курсовой устойчивости.
- Уменьшение срока службы ступичных подшипников.
- Повышенный износ шин.
- Увеличения усилия при повороте руля.
- Уменьшение срока службы ходовой.
Как измеряется вылет диска
Бывает, что прочитать маркировку с вылетом физически невозможно. К примеру, если в ваших руках оказался старый колесный диск. Определить величину вылета поможет нехитрая инструкция:
- Уложите диск лицевой стороной на ровную поверхность.
- Положите ровную планку на обод (проводить эту процедуру удобнее при демонтированной шине).
- Измерьте расстояние от привалочной плоскости до нижнего края планки.
- Запишите это расстояние как «А».
- Переверните колесо.
- Аналогичным образом измерьте расстояние от привалочной поверхности до планки, используя рулетку.
 Запишите значение как «В».
Запишите значение как «В». - Рассчитайте вылет по формуле: ET= (A+B)/2–B.
Во время измерения не пренебрегайте точностью. Напомним, речь идет о миллиметрах!
Существует еще один способ замера вылета диска. Выполняется он аналогичным образом — с помощью ровной планки и линейки:
- Уложите колесо «лицом» на ровную поверхность.
- Приложите ровную планку к внешней стороне.
- Измерьте расстояние от опорной поверхности до нижнего края планки (от лицевого до изнаночного борта) — «В».
- Измерьте расстояние от опорной поверхности до плоскости, которая соприкасается со ступицей автомобиля — «А».
- Рассчитайте вылет по формуле: ET=А–В/2. Результаты могут быть как положительными или отрицательными, так и нулевыми.
Схема примерно такая:
Таблица вылета дисков
На практике большинство автопроизводителей допускает незначительное отклонение от заводских параметров вылета как в большую, так и в меньшую сторону. Однако, обычно речь идет не более, чем о 5–7 мм.
Однако, обычно речь идет не более, чем о 5–7 мм.
Как подобрать диски по вылету
Подбирая колесные диски, в первую очередь нужно обратиться к инструкции транспортного средства и лишь в крайнем случае прибегать к экспериментам. Иногда найти и приобрести диски с «заводским» ET невозможно, к примеру, если речь идет о старой или редкой машине. Можно попытаться устранить несоответствие с помощью специальных проставок — металлических колец определенной толщины, которые устанавливаются между диском и ступицей. В остальных случаях можно воспользоваться таблицей допустимых значений.
Если по какой-то причине найти диски с минимальным отклонением от рекомендованного значения вылета вам так и не удалось, то перед покупкой дисков обязательно примерьте их на автомобиле: такие диски могут физически не подойти.
Вячеслав Субботин, директор гоночной команды «ГАЗ Рейд Спорт» и автор программы «Минтранс» на телеканале РЕН ТВ:
«Ставить нужно только те колесные диски, которые рекомендованы автопроизводителем — с правильным вылетом. Это влияет на управляемость автомобиля. Если посмотреть на какую-нибудь тюнингованную «девятку» с громадным отрицательным вылетом, у которой колеса вылезают наполовину крыла, то перед вами неуправляемая машина — ее надо опасаться.
Это влияет на управляемость автомобиля. Если посмотреть на какую-нибудь тюнингованную «девятку» с громадным отрицательным вылетом, у которой колеса вылезают наполовину крыла, то перед вами неуправляемая машина — ее надо опасаться.
То же самое касается внедорожников. При таком тюнинге всегда изменяется плечо обкатки — руль будет просто вырываться из рук. В ключевой момент невозможно будет удержать автомобиль. Машина не управляется, вот и всё!
Вылет устанавливается производителем для того, чтобы была хорошая управляемость и курсовая устойчивость, чтобы была стабильность в поворотах. Ни в коем случае ни в плюс, ни в минус уходить не нужно. Люди делают это для красоты, не понимая того, что происходит. Мало того, сильно нагружаются ступичные подшипники. Очень сильно! Они довольно быстро выходят из строя. Изгибающий момент хлоп по подшипнику — и его нет! Даже в маленькой ямке.
Если проехать на нормальных колесах с нормальным вылетом по этой же ямке, возможно, ничего не случится. А с неправильным вылетом — одни проблемы.
А с неправильным вылетом — одни проблемы.
И последнее. Поворотные кулаки на современных автомобилях делают непонятно из чего — безо всякого запаса прочности. Это подтверждает опыт каршеринга: когда машины приезжают в сервис, у них колеса домиком стоят, потому что поворотные кулаки гнутые. Даже диски целые, а кулаки гнутые. С неправильным вылетом нагрузка идет и на поворотный кулак. А это — серьезные последствия».
Список рекомендация касательно вылета колесных дисков предельно краток:
- Устанавливайте диски с ET, рекомендованным автопроизводителем.
- При невозможности найти оригинальные диски, попытайтесь компенсировать несоответствие вылета с помощью проставок.
- В крайнем случае устанавливайте диски с минимальным отклонением по вылету от заводских значений — параметр не должен отличаться более чем на 10 мм. Чем меньше разница с «заводом», тем лучше.
- Как получить, заменить и восстановить водительское удостоверение
- Низко и медленно: что такое лоурайдеры и как они устроены
- «Русский Hummer», «Гном» и другие легковушки КамАЗа
www. adv.rbc.ru
adv.rbc.ru
www.adv.rbc.ru
Цифры и буквы в маркировке диска
Каждый производитель автомобилей настоятельно рекомендует определённый тип размера диска, эти данные можно получить в сервисной книжке или на наклейке в проёме водительской двери рядом с информацией о размере и давлении шин. Несоблюдение этих требований может повлиять на ходовые качества автомобиля или на быстрый износ подвески. Выбирая диски на автомобиль, надо уметь «читать» цифры и буквы в маркировке.
Рассмотрим маркировку дисков на примере популярного на сегодняшний день автомобиля Kia Rio new. Производитель рекомендует для установки диски 6J15 PCD4-100 et48 DIA 54,1. Давайте разберёмся и расшифруем эту надпись, а для начала глянем на главные размеры диска.
6J15
Цифра 6 означает, что ширина обода равна шести дюймам. J– указывает, что размер дан в дюймах, 15 – это диаметр обода в дюймах.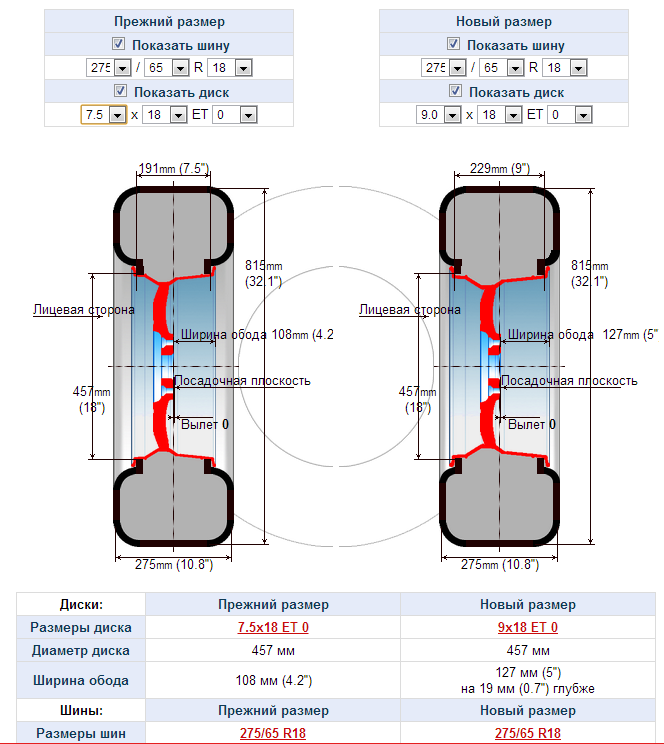
PCD 4-100
Эти цифры указывают, что на диске 4 отверстия под болты крепления и межболтовое расстояние 100 миллиметров.
Et-48
Самый важный параметр указывает «вылет» диска. Не соблюдение этого параметра может впоследствии повлечь за собой много проблем.
Вылет меньше рекомендованного делает колёсную базу шире, увеличивая тем самым нагрузку на подвеску из-за смещения центра тяжести колеса. Также при уменьшении вылета колёса могут задевать за арки крыльев. Вылет больше рекомендованного смещает колёса вовнутрь, уменьшая тем самым устойчивость автомобиля. Также при увеличенном вылете колёсный диск может цеплять суппорт. Не поддавайтесь на ухищрения продавцов, выбирайте вылет, указанный производителем вашего автомобиля.
DIA 54,1
Это посадочный диаметр диска. Если это значение меньше указанного производителем, диск просто не налезет на ступицу. Когда это значение больше – это не так страшно, такой диск можно установить, но потребуются проставочные (центровочные) кольца.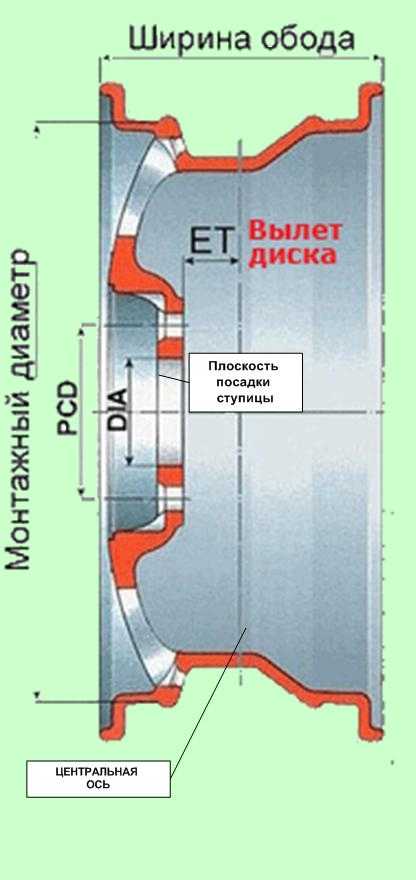 Следует учесть, что даже при применении проставочных колец может наблюдаться дисбаланс отбалансированного колеса.
Следует учесть, что даже при применении проставочных колец может наблюдаться дисбаланс отбалансированного колеса.
Некоторые специалисты полагают, что центровочные кольца – аксессуар бесполезный. Почему? Дело в том, что центральное отверстие и его диаметр не играют совершенно никакой роли в центровке и фиксации колеса. Колесо центрируется и фиксируется только конусной частью болтов, и ничем иным.
Ставим штатный диск (диаметр его центрального отверстия совпадает с диаметром выступающей части ступицы) на ступицу и затягиваем болты с конусами (с конусными гайками всё обстоит точно так же). Колесо село на своё место безупречно, тут никаких вопросов нет.
Теперь берем диск с отверстием нештатного, увеличенного размера, и ставим на ступицу без центровочного кольца. Неидеально, со смещением.
Затягиваем болты спокойно, равномерно, крест-накрест ручным ключом – без пневмогайковерта, способного иногда перекосить диск. Конусы болтов входят в конусы отверстий, и колесо автоматически встаёт строго по центру ступицы вне зависимости от наличия или отсутствия центровочного кольца и вне зависимости от диаметра центральной «дырки» в диске, которая может быть любой!
Центровка конусами (или полусферами) – это старый, проверенный и очень часто применяемый в самых разнообразных механизмах приём, и в случае c колёсами он использован в полной мере.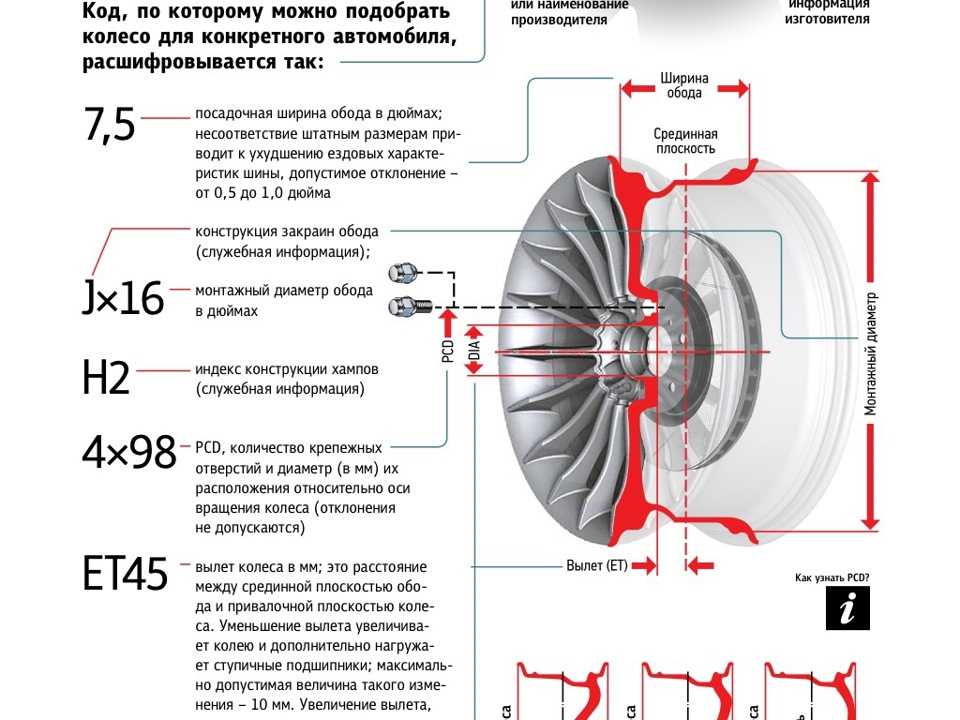 Центровка диска центральным отверстием не дополняет конусный крепёж, она просто не предусмотрена инженерами, которые проектировали автомобиль.
Центровка диска центральным отверстием не дополняет конусный крепёж, она просто не предусмотрена инженерами, которые проектировали автомобиль.
Впрочем, помимо центровки «сферически в вакууме» популярный миф о центровочных колечках затрагивает поведение колеса в движении. Многим кажется, что из-за пустоты в том месте, где якобы должно находиться центровочное кольцо, диск может сместиться относительно ступицы от воздействия массы машины и езды по неровностям. Что появится дисбаланс, биение. Отсюда возникает умозаключение, что кольцо выполняет не только центрирующую, но и опорную роль.
Это ещё более чудовищное заблуждение, которое легко развеивается, стоит только представить себе воздействующие (теоретически!) на центровочное кольцо силы, если бы оно выполняло опорную роль.
Из чего изготавливаются кольца? Из тоненького пластика или алюминия, то есть из чрезвычайно мягких и пластичных материалов, категорически неспособных держать нагрузки, даже отдалённо сходные с теми, которые испытывает колёсный диск в движении.
Получается, что на кольцо действуют чудовищные силы, приложенные к очень небольшой площади. Если бы проставка из пластикового колечка на самом деле выполняла хоть малейшую опорную роль, она должна была быть выполнена из прочной стали. А пластик или алюминий на первых же нескольких кочках серьёзно бы деформировало – так, что повреждения нельзя было бы не заметить невооруженным глазом.
Однако после любого пробега даже хилая полиэтиленовая проставка не несёт на себе никаких следов давления и ударов… Причина в том, что центруют и держат колесо исключительно конусные поверхности болтов, и только они. Роль кольца равна нулю, оно не влияет ни на биение колеса, ни на прочность крепления.
Поэтому можно спокойно приобретать и ставить нештатные колёса, если они устраивают вас по цене и подходят по всем размерным параметрам, кроме диаметра центрального отверстия. Никакие «центровочные кольца» для компенсации увеличенного отверстия не нужны.
Однако существуют хитрые болты крепления колёс – со скользящими эксцентрическими конусами.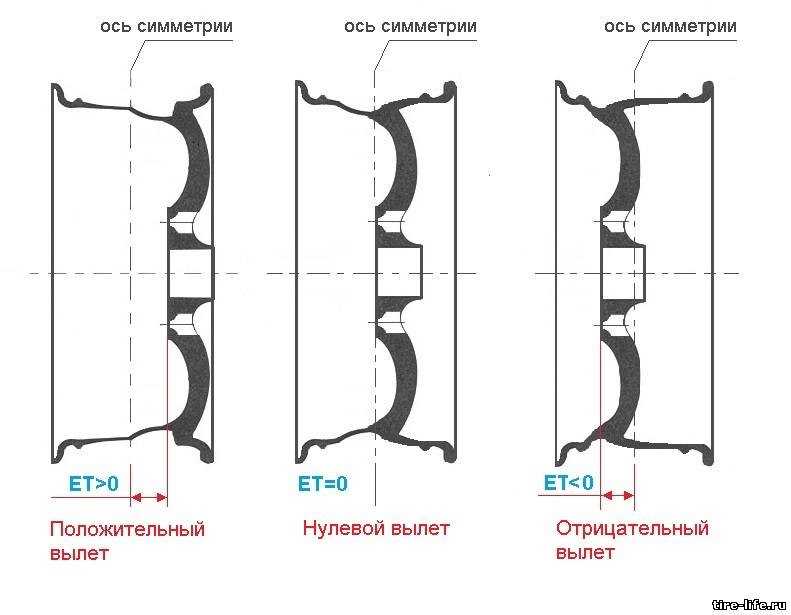 Это тюнинговый аксессуар, позволяющий совместить ступицу и колесо с разной разболтовкой без заваривания и пересверливания отверстий, и без «блинов», меняющих вылет. Например, поставить на ступицы 4х98 колёса 4х100. Такие хитрые болты – не самое лучше техническое решение, но, тем не менее, оно существует и иногда используется. Чтобы с такими болтами смонтировать без перекоса колесо, диаметр центрального отверстия которого больше ступицы, крайне желательно использовать центрирующее кольцо. В подобных случаях желательны центрирующие кольца для литых дисков из термостойкого поликарбоната и алюминия.
Это тюнинговый аксессуар, позволяющий совместить ступицу и колесо с разной разболтовкой без заваривания и пересверливания отверстий, и без «блинов», меняющих вылет. Например, поставить на ступицы 4х98 колёса 4х100. Такие хитрые болты – не самое лучше техническое решение, но, тем не менее, оно существует и иногда используется. Чтобы с такими болтами смонтировать без перекоса колесо, диаметр центрального отверстия которого больше ступицы, крайне желательно использовать центрирующее кольцо. В подобных случаях желательны центрирующие кольца для литых дисков из термостойкого поликарбоната и алюминия.
Вне зависимости от того, умеете вы читать маркировку дисков колёс для автомобиля или нет, за руль имеет право садиться лишь тот, кто обладает водительскими правами. Когда последние ещё и международного образца, это крайне удобно и практично. Международное водительское удостоверение легко оформить на нашем сайте. Не упускайте такую возможность!
Вылет дисков — Шины и диски
-
04.
 06.2008, 22:10
#1
06.2008, 22:10
#1
Вылет дисков
Как узнать свой вылет, обозначения на диске — http://www.shinamall.ru/markorovka_diskov.php
статья о том чем чревато смена вылета — http://www.shinaexpert.ru/articles/6740.html
еще понятная статья — http://mondeoclub.ru/remont/vulet.htmкалькулятор вылета — http://www.1010tires.com/WheelOffsetCalculator.asp Как им пользоваться?
значит так:Current Wheel Specs — ширина (например J5.5 J6 J7.5) и вылет (25-45 mm) вашего заводского диска
New Wheel Specs тоже самое для нового диска, который хотите поставитьзадаем параметры и жмем calculate!
Ниже два параметра это:
Outer Position: — изменение расстояние до крыла по отношению к заводским дискам (как правило пишет прибавку) «EXTEND an extra 26mm» (больше на 26 мм)Вот я например хочу сменить диски с ширины J5.
 5 на J6.5 какой вылет должен быть у новых дискав, что бы они не терлись об внутренности подвески? поиграв с вылетом моего будущего колеса получаем значение — 32 мм, т.е. был вылет 45 а нужен теперь 32.
5 на J6.5 какой вылет должен быть у новых дискав, что бы они не терлись об внутренности подвески? поиграв с вылетом моего будущего колеса получаем значение — 32 мм, т.е. был вылет 45 а нужен теперь 32.В догонку — шинный калькулятор — http://www.best-tyres.ru/tyres/calculator
-
-
05.06.2008, 15:57 #2
Вылет дисков
Внимательно пользуйтесь поиском, тут эта тема поднималась не раз и вся информация по ней подробно предоставлена.
Для примера приведу замену колес на своем авто
было: 4х114.3 6J15 ЕТ=45 ЦО=66.1
стало: 4х114,3 7J16 ET=43 ЦО=73.0
Как видно ширина диска увеличилась на дюйм,а вылет изменился на 2мм.
Насчет твоего вопроса я честно говоря не особо понял ты собираешься меня 5. 5 на 6.5 одного диаметра или же будет переход на больший?
5 на 6.5 одного диаметра или же будет переход на больший?
-
05.06.2008, 16:28 #3
Вылет дисков
На больший диаметр, но не изменяя общего диаметра вместе с покрышкой.
Я вижу так:
сейчас — R14 J5.5 185/65
хочу R15 J6.5 195/55по идее (теоретически) мое колесо изменится только выступив на 26 мм от кузова. Вот только вылет смущает, слишком сильно изменился. Просто я не вкурсе есть там место во внутрь или нет.
-
05.06.2008, 18:08 #4
Вылет дисков
Давай начнем с того что такое вылет (ЕТ)
Это расстояние между продольной плоскостью симметрии обода и крепежной (привалочной) плоскостью колеса. Вылет может быть нулевым, положительным (ступица диска выпячена наружу относительно середины обода) и отрицательным (ступица утоплена).
Вылет может быть нулевым, положительным (ступица диска выпячена наружу относительно середины обода) и отрицательным (ступица утоплена).
Грубо говоря имея стандартный ЕТ=45, установить диск с вылетом >45 не представляется возможным(за исключением дисков с выпуклыми спицами), так как диск при установке упрется в тормозной суппорт, следовательно вылет можно только уменьшать. Для начала стоит посмотреть какие варианты колесных дисков устанавливались на твою машину на заводе(ширина и диаметр),и я более чем уверен что при разной ширине и разном диаметре они имели одинаковый ЕТ, исключения составляют диски с диаметром от 16, так как они изначально имеют большую ширину нежели 14 и 15. От себя скажу при замене 5.5 на 6.5 вылет необходимо уменьшить (а можно и оставить таким же) на 2-5мм. Больше не стоит,так как смысла не имеет особенно учитывая ширину резины 195. А вообще не стоит с ЕТ перебарщивать, максимально допустимое изменение 10 мм и то для 17-х катков при ширине 7 и 7,5J.
Твой вариант при замене 4х114,3 6. 5J R15 ET=43 (до 40) встанет без проблем.
5J R15 ET=43 (до 40) встанет без проблем.
-
06.06.2008, 01:05 #5
Вылет дисков
посмотрел щас на размер ГТ — J6 там ставили на заводе а 15 радиус на счет ЕТ не знаю, вообщем проще самому посмотреть влезут диски или нет, залезть под машину и померить с каждой стороны от колеса.
Кстати, значения ширины это в дюймах? например J6 это шесть дюймов? Мало что-то, может от ценра? т.е. всего 12 дюймов? как это значение в см перевести?
ПС: я вообще хочу расширить диски для лучшего сцепления. а то надоело с пробуксовкой стартовать. (не специально) -
06.06.2008, 21:53 #6
Вылет дисков
Ну насчет того что бы померить влезут или нет это без сомнений делается на месте,а вот измерять расстояние от элементов подвески до предполагаемой ширины.
 …….все равно будет очень приблизительно. Покрышка шириной 195 оптимальна садиться на диск шириной 6.5J, я ставил и на родную 6J-все без проблем. Могу даже почти на 100% сказать что при ширине покрышки 195 и диска 6Jx15 все встанет без проблем на ЕТ=45. Почему «почти», так как ставил на р11,но если не изменяет память на р10 все тоже самое.
…….все равно будет очень приблизительно. Покрышка шириной 195 оптимальна садиться на диск шириной 6.5J, я ставил и на родную 6J-все без проблем. Могу даже почти на 100% сказать что при ширине покрышки 195 и диска 6Jx15 все встанет без проблем на ЕТ=45. Почему «почти», так как ставил на р11,но если не изменяет память на р10 все тоже самое.
-
04.12.2008, 15:45 #7
Вылет
Сорри, если где-то обсуждалось уже… полистал — не нашел.
Решил подобрать на лето новые диски на свою Р10 (с зимы, так сказать, заранее колеса подготовить…)
Согласно паспорту, диски нужны следующей геометрии:5.5JJx14
— крепёжные отверстия (PCD), мм: 4*114.3
— вылет (ET), мм: 45
— диаметр ступичного отверстия (DIA), мм: 66В магазине обнаружил нужные диски, но с меньшим вылетом — 35мм.

Напрашивается вопрос. Подскажите, подойдут ли мне такие? И можно ли ставить диски с меньшим вылетом? И на чем это скажется в поведении машины? Продавцы говорят, что ставить можно, ничего страшного.
(я так понимаю, что просто колея расширится на 20мм, и возможно поворачивать станет каплю труднее…)Вроде уже давно тут а поиском почему не пользуешься? Объеденил с темой Вылет Дисков
√O√ANыч -
04.12.2008, 15:57 #8
Вылет
сдесь почитай: http://www.shina54.ru/articles/
а вообще это уже обсуждалось тыщу раз, внимательнее нужно быть -
04.12.2008, 15:58 #9
Вылет
http://www.
 primera-club.ru/forum/board/21.htm
primera-club.ru/forum/board/21.htm
-
04.12.2008, 16:05 #10
Вылет
Пока вычитал это:
Предупреждение! Не ставьте на автомобиль колеса с нештатным вылетом. Уменьшение вылета делает колею колес шире; хотя это немного и повышает устойчивость автомобиля и придает ему стильный гоночный вид, но вместе с тем резко перегружает подшипники ступиц и подвеску. Увеличить же вылет, т.е. сузить колею , как правило, невозможно — диск упрется в тормоз.Неужели 10мм так сильно повлияют ?
Кстати говоря, с уменьшением вылета (положительного) я так понимаю, нагрузка на подшипник наоборот должна уменьшаться. Ибо точка центра давления как раз приближается к центру ступицы :-\
(в данном конкретном случае, если рассматривать Р10)
Ведь я ставлю вылет не 0мм вместо положенных, скажем, 60 , а всего лишь 35 вместо 45. ..
..
Где на дисках пишется маркировка у колеса (расшифровка значений)
Главная » Эксплуатация » Шины
На чтение 7 мин. Просмотров 3.6k. Опубликовано Обновлено
Рынок автомобилей всегда рад предложить покупателям аксессуары на любой вкус и кошелек. Это же касается и колес. В этой статье вы узнаете, где на дисках пишется маркировка и как узнать размер диска на авто, чтобы подобрать наиболее оптимальную конфигурацию и избежать ошибок.
Содержание
- Где на дисках пишется маркировка
- Как узнать размер диска на автомобиле
- Как расшифровать параметры диска
- Пример маркировки модели 7jx15h3/112 ET45 d 66.
 6
6 - Пример маркировки модели КрКЗ UA160651/ 2 Jxh3 ET47 560 226.15
- Вылет диска: что это и за что отвечает
- Как выбрать диски для автомобиля
- Как правильно читать обозначения на дисках автомобиля – видео
Где на дисках пишется маркировка
Маркировку покрышек машин можно разделить на два типа: обычный и дополнительный.
- Обычная маркировка – это данные о разъемности и ширине обода, его выступах и вылете, разновидности его кромки и диаметре (D).
- Дополнительная маркировка – это сведения о наивысшей нагрузке, предельном давлении в шине, способах изготовления диска, а также информация про сертификацию изделия. При этом не на каждой модели есть все выше перечисленные данные.
На изделиях литого типа маркирование делают на спицах или между спицами на внешней стороне. Все сильно зависит от определенной модели. Надписи часто есть внутри спиц. По всей окружности крепежного отверстия под гайку ступицы, между специальными отверстиями для болтов, наносятся определенные данные касательно размера и параметров изделия.
Что такое специальные штампы на машине
Это самая простая и бюджетная разновидность покрышек. На изделиях штампованного типа маркирование находится на поверхности с внешней или внутренней стороны. Сегодня есть два вида нанесения. Первый — надписи наносят на участок между специальными отверстиями для крепежа. Второй – данные указываются по всему периметру обода вблизи его внешнего края.
Как узнать размер диска на автомобиле
Как можно узнать какая сверловка на дисках? Все очень просто. Размеры литых моделей зависят от их диаметра. Последний можно легко увидеть на маркировании боковины шины. После буквы R находится число, которое означает диаметр изделия.
Диаметр часто указывают на маркировке внутри покрышки.
Как расшифровать параметры диска
Множество параметров автодисков непосредственно влияет на время функционирования подвески без потребности в ремонте и безопасность езды. Выбирая такие изделия, важно знать, модели с какими параметрами можно монтировать на транспортное средство. Лишь при полном соответствии ряда требований вы можете устанавливать колесо на авто.
Лишь при полном соответствии ряда требований вы можете устанавливать колесо на авто.
Умение быстро и легко читать маркирование дает возможность выбирать колеса к машине правильно и без ошибок. Важно только верно распознавать на изделии все обозначения.
Пример маркировки модели 7jx15h3/112 ET45 d 66.6
Рассмотрим маркирование колеса: 7jx15h3/112 ET45 d 66.6:
- 7,5 — ширина покрышки в дюймах.
- J — эта латинская буква означает кое-какие особенности конструкции колеса и не имеет большого значения.
- x — изделие нераздельное.
- 15 — посадочный D модели, который соответствует посадочному D покрышки.
- Н2 — наличие на полках обода двух хампов.
- 5/112 — PCD (сверловка колесных автомобильных дисков). Цифра 5 – это число отверстий для различных гаек и болтов. Цифра 112 — это D окружности в мм, на которой они находятся.
- ET 45 — вылет у изделия положительный.
 Его размер 45 мм.
Его размер 45 мм. - d 66.6 — данный параметр определяет D центрального отверстия (DIA).
Пример маркировки модели КрКЗ UA160651/ 2 Jxh3 ET47 560 226.15
Рассмотрим маркирование модели: КрКЗ UA160651/ 2 Jxh3 ET47 560 226.15:
- КрКЗ — Кременчугский колесный завод.
- UA — Украина.
- 16 06 — дата изготовления июнь 2016 г.
- 5 1 / 2 — ширина наружной части изделия – 5,5 дюйма.
- J — вид бортовой закраины наружной части изделия.
- x — неразъемный обод.
- h3 — тип посадочных полок. Латинская буква H обозначает наличие выступа для установки шин без камер. Число 2 – выступ есть внутри и снаружи обода.
- ЕТ47 — вылет колеса составляет 47 мм.
- 560 — наибольшая нагрузка на модель составляет 560 кг.
- 226.15 — фабричная маркировка модели.

Помимо такого маркирования, на модель наносят следующие условные обозначения:
- LZ — обозначение общего числа отверстий для крепежа.
- DIA — диаметр основного отверстия.
- PCD — pcd на дисках колес что это? Это диаметр расположения всех отверстий.
Вылет диска: что это и за что отвечает
Вылет – дистанция между вертикальной плоскостью симметрии модели и плоскостью приложения покрышки к ступице.
Вылет – это крайне важная характеристика. Ведь если он не будет подходить по диаметру и общему количеству отверстий для болтов, то вмонтировать такую покрышку будет невозможно. Модель с неподходящим стандартному вылету часто легко можно установить на ступицу и вроде бы он будет выполнять задачи вполне нормально. Но так ли это?
Вылет покрышки должен подходить требованиям изготовителя машины. Каких-либо отклонений в любые стороны здесь не может быть в принципе.
Как выбрать диски для автомобиля
Приобретение новых дисков – это достаточно редкое событие. Для такой покупки есть несколько причин:
- У колес, которые используются в автомобиле есть существенные повреждения.
- Новые покрышки покупают в качестве запасных.
- Хороший метод изменения внешнего вида транспортного средства.
Чтобы правильно выбрать такой товар, потребуется смотреть не только на их внешний вид, но и на целый ряд технических параметров:
- Диаметр. Это цифра из двух значений в дюймах, которая должна быть аналогичной посадочному размеру покрышки. Покупка колес по марке машины не обходится без официального руководства. Там можно найти все подходящие размеры. Если в инструкции к автомобилю указано, что подходящие колеса – модели с диаметром 15-17 дюймов, то изделие на 18 дюймов будет уже мешать элементам тормозов при поворотах либо тереться об арку покрышки. А колесо на 13 дюймов существенно ухудшит управляемость.
 Машина станет более валкой.
Машина станет более валкой. - Диаметр посадочного отверстия (цо на дисках). Этот параметр обозначают буквой из латиницы D. Он должен быть аналогичным размерам ступицы машины. Если необходимого вам диаметра нет в наличии, лучше купить большее изделие, потому что его легко вмонтировать специальным инструментом.
- Наибольшая нагрузка. Этот параметр показывает какой предельный вес может выдержать одна модель.
- Форма отверстий для крепежей. Для современных легкосплавных типов используются длинные болты с наконечниками в виде конуса, а для штампованных — короткие болты с плоскими головками.
- Ширина. В маркировании она отмечается буквой J. Посадочное место колеса должно быть на четверть меньше общей ширины протектора. При этом важно понимать, что габариты шин и колес часто указаны в различных измерительных единицах.
- Отверстия для крепежей. Важно обязательно смотреть на количество болтов и дистанцию до самого центра ступицы транспортного средства, на которую непосредственно устанавливается покрышка.

- Вылет (ET). Это одна из наиболее важных стадий покупки. Вылет – дистанция от середины обода изделия до плоскости, прилегающей к ступице транспортного средства. Если в маркировке нет этих двух букв, значит нужно искать слово Offset. Его сегодня применяют такие производители, как 5Zigen и Alutec. Французские фирмы штампуют обозначение Deport. Чем колесный вылет крупнее, тем больше внутри колеса поместится различных деталей и узлов. Важно подбирать изделия по тем характеристикам, которые описаны в руководстве либо по габаритам ранее установленных механизмов и узлов.
- Наличие хампов. Это специальные выступы для лучшей фиксации шин без камер. Они есть у подавляющего большинства дисков.
- Дизайн. На современных спортивных машинах очень будут хорошо смотреться ажурные изделия с красивыми спицами. Для внедорожников лучше выбирать более крупные модели.
- Цвет. Наиболее часто покрышки приобретают цвет прямо на производственной линии.
 Вы можете купить покрышки под оттенок кузова либо подобрать какой-то контрастный оттенок.
Вы можете купить покрышки под оттенок кузова либо подобрать какой-то контрастный оттенок.
Как правильно читать обозначения на дисках автомобиля – видео
Выбирать диск автомобильного колеса необходимо по технических сведениях, которые предоставляет производитель транспортного средства. В том числе, по габаритам покрышек определенной марки автомобиля, их типам, диаметрам отверстий и значениям вылетов. На подавляющее большинство машин можно устанавливать покрышки разных диаметров. Но их главные характеристик должны непременно соответствовать официальным документам.
Оцените автора
Систематический литературный обзор особенностей визуализации дегенерации позвоночника у бессимптомных групп населения
1. Ярвик Дж.Г., Дейо Р.А. Диагностическая оценка болей в пояснице с упором на визуализацию. Энн Интерн Мед
2002;137:586–97 [PubMed] [Google Scholar]
Ярвик Дж.Г., Дейо Р.А. Диагностическая оценка болей в пояснице с упором на визуализацию. Энн Интерн Мед
2002;137:586–97 [PubMed] [Google Scholar]
2. Дейо Р.А., Черкин Д., Конрад Д. и др.. Стоимость, полемика, кризис: боль в пояснице и здоровье населения. Анну Рев Общественное здравоохранение 1991;12:141–56 [PubMed] [Google Scholar]
3. Ли А.Л., Йен Д. Влияние увеличения использования МРТ и КТ на принятие клинических решений у пациентов, направленных в хирургическую клинику по поводу болей в спине. Джан Джей Сург 2011; 54:128–32 [бесплатная статья PMC] [PubMed] [Google Scholar]
4. Carragee E, Alamin T, Cheng I, et al. Связаны ли первые эпизоды серьезной БНС с новыми данными МРТ? Позвоночник J 2006; 6: 624–35 [PubMed] [Google Scholar]
5. Боден С.Д., Дэвис Д.О., Дина Т.С. и др. Аномальные магнитно-резонансные томограммы поясничного отдела позвоночника у бессимптомных субъектов: проспективное исследование. J Bone Joint Surg Am 1990; 72:403–08 [PubMed] [Google Scholar]
6. Каличман Л., Ким Д.Х., Ли Л. и др.. Особенности дегенерации позвоночника, оцененные с помощью компьютерной томографии: распространенность, взаимосвязь и связь с самоотчетами о боли в пояснице. Позвоночник J
2010;10:200–08 [бесплатная статья PMC] [PubMed] [Google Scholar]
Каличман Л., Ким Д.Х., Ли Л. и др.. Особенности дегенерации позвоночника, оцененные с помощью компьютерной томографии: распространенность, взаимосвязь и связь с самоотчетами о боли в пояснице. Позвоночник J
2010;10:200–08 [бесплатная статья PMC] [PubMed] [Google Scholar]
7. Визель С.В., Цурмас Н., Феффер Х.Л. и др. Исследование компьютерной томографии. I. Частота положительных результатов компьютерной томографии в бессимптомной группе пациентов. Позвоночник (Фила Па, 1976) 1984; 9: 549–51 [PubMed] [Google Scholar]
8. Фардон Д. Ф., Милетт ПК. Номенклатура и классификация патологии поясничного диска: рекомендации объединенных целевых групп Североамериканского общества позвоночника, Американского общества радиологии позвоночника и Американского общества нейрорадиологии. Позвоночник (Фила Па 1976) 2001;26:E93–E113 [PubMed] [Google Scholar]
9. Sasiadek MJ, Bladowska J. Визуализация дегенеративных заболеваний позвоночника – современное состояние. Adv Clin Exp Med 2012;21:133–42 [PubMed] [Google Scholar]
10. Berg L, Hellum C, Gjertsen O и др. Означают ли дополнительные результаты МРТ ухудшение инвалидности или более интенсивную боль в пояснице? Поперечное исследование кандидатов на протезирование поясничного диска. Скелетный радиол
2013;42:1593–602 [PubMed] [Google Scholar]
Berg L, Hellum C, Gjertsen O и др. Означают ли дополнительные результаты МРТ ухудшение инвалидности или более интенсивную боль в пояснице? Поперечное исследование кандидатов на протезирование поясничного диска. Скелетный радиол
2013;42:1593–602 [PubMed] [Google Scholar]
11. Takatalo J, Karppinen J, Niinimäki J, et al. Ассоциация изменений Modic, узлов Шморля, спондилолитических дефектов, поражений зоны высокой интенсивности, грыж дисков и радиальных разрывов с тяжестью симптомов поясничного отдела позвоночника у молодых взрослых финнов. Позвоночник (Фила Па 1976) 2012;37:1231–39 [PubMed] [Google Scholar]
12. Стеффенс Д., Хэнкок М.Дж., Махер К.Г. и др. Предсказывает ли магнитно-резонансная томография будущую боль в пояснице? Систематический обзор. евро J боль 2014;18:755–65 [PubMed] [Google Scholar]
13.
Kovacs FM, Arana E, Royuela A, et al.. Изменения замыкательной пластинки позвонков не связаны с хронической болью в пояснице у субъектов из Южной Европы: исследование случай-контроль. AJNR Am J Нейрорадиол
2012;33:1519–24 [бесплатная статья PMC] [PubMed] [Google Scholar]
AJNR Am J Нейрорадиол
2012;33:1519–24 [бесплатная статья PMC] [PubMed] [Google Scholar]
14. Канеока К., Симидзу К., Хангай М. и др.. Дегенерация поясничного межпозвонкового диска у элитных пловцов-профессионалов: исследование случай-контроль. Am J Sports Med 2007; 35:1341–45 [PubMed] [Google Scholar]
15. Kraft CN, Pennekamp PH, Becker U, et al. Результаты магнитно-резонансной томографии поясничного отдела позвоночника у элитных всадников: корреляция с болью в спине, индексом массы тела, коэффициентом длины туловища/ноги и дисциплиной верховой езды. Am J Sports Med 2009; 37:2205–13 [PubMed] [Google Scholar]
16. Modic MT, Obuchowski NA, Ross JS, et al. Острая боль в пояснице и радикулопатия: данные МРТ, их прогностическая роль и влияние на исход. Радиология 2005; 237:597–604 [PubMed] [Google Scholar]
17. Чоу Р., Фу Р., Каррино Дж. А. и др. Стратегии визуализации при боли в пояснице: систематический обзор и метаанализ. Ланцет 2009; 373:463–72 [PubMed] [Google Scholar]
18. Карлайл Э., Луна М., Цоу П.М. и др.. Процент компрометации позвоночного канала на МРТ, используемый для прогнозирования необходимости хирургического лечения при одноуровневой поясничной грыже межпозвонкового диска. Позвоночник J
2005; 5: 608–14 [PubMed] [Google Scholar]
Карлайл Э., Луна М., Цоу П.М. и др.. Процент компрометации позвоночного канала на МРТ, используемый для прогнозирования необходимости хирургического лечения при одноуровневой поясничной грыже межпозвонкового диска. Позвоночник J
2005; 5: 608–14 [PubMed] [Google Scholar]
19. Лурье Д.Д., Мозес Р.А., Тостесон А.Н. и др. Магнитно-резонансная томография предикторы хирургического исхода у пациентов с поясничной грыжей межпозвонкового диска. Позвоночник (Фила Па, 1976) 2013;38:1216–25 [бесплатная статья PMC] [PubMed] [Google Scholar]
20. Гринберг Дж.О., Шнелл Р.Г. Магнитно-резонансная томография поясничного отдела позвоночника у бессимптомных взрослых: совместное исследование — Американское общество нейровизуализации. J Нейровизуализация 1991; 1:2–7 [PubMed] [Google Scholar]
21.
Терагути М., Йошимура Н., Хасидзуме Х. и др.. Распространенность и распространение дегенерации межпозвоночных дисков по всему позвоночнику в популяционной когорте: исследование позвоночника Вакаямы. Остеоартрит Хрящ
2014; 22:104–10 [PubMed] [Google Scholar]
Остеоартрит Хрящ
2014; 22:104–10 [PubMed] [Google Scholar]
22. Джарвик Дж. Дж., Холлингворт В., Хегерти П. и др. Исследование «Продольная оценка визуализации и инвалидности спины» (LAIDBack): исходные данные. Позвоночник (Фила Па, 1976) 2001;26:1158–66 [PubMed] [Google Scholar]
23. Jarvik JG, Hollingworth W, Heagerty PJ и др. Трехлетняя заболеваемость болью в пояснице в изначально бессимптомной когорте: клинические и визуализирующие факторы риска. Позвоночник (Фила Па, 1976) 2005;30:1541–48; обсуждение 1549 [PubMed] [Google Scholar]
24. Арана Э., Ковач Ф.М., Ройуэла А. и др.. Влияние номенклатуры на интерпретацию контура поясничного диска на МРТ: сравнение согласия с использованием объединенной рабочей группы и скандинавских номенклатур. AJNR Am J Нейрорадиол 2011;32:1143–48 [бесплатная статья PMC] [PubMed] [Google Scholar]
25.
Arana E, Royuela A, Kovacs FM и др.. Поясничный отдел позвоночника: согласие в интерпретации 1,5-T MR-изображений с использованием формы классификации Nordic Modic Consensus Group. Радиология
2010;254:809–17 [PubMed] [Google Scholar]
Радиология
2010;254:809–17 [PubMed] [Google Scholar]
26. Торнтон А., Ли П. Предвзятость публикации в метаанализе: ее причины и последствия. Дж. Клин Эпидемиол 2000; 53: 207–16 [PubMed] [Google Scholar]
27. Боден С.Д., Рью К.Д., Ямагути К. и др. Ориентация поясничных фасеточных суставов: связь с остеохондрозом. J Bone Joint Surg Am 1996;78:403–11 [PubMed] [Google Scholar]
28. Боос Н., Ридер Р., Шаде В. и др. Премия Volvo 1995 г. в области клинических наук: диагностическая точность магнитно-резонансной томографии, восприятие работы и психосоциальные факторы при выявлении симптоматических грыж диска. Позвоночник (Фила Па, 1976) 1995;20:2613–25 [PubMed] [Google Scholar]
29. Капель А., Медина Ф.С., Медина Д. и др. Магнитно-резонансное исследование поясничных дисков у танцовщиц. Am J Sports Med 2009; 37:1208–13 [PubMed] [Google Scholar]
30.
Дэниелсон Б., Уиллен Дж. Магнитно-резонансное изображение поясничного отдела позвоночника с осевой нагрузкой у бессимптомных людей. Позвоночник (Фила Па, 1976)
2001;26:2601–06 [PubMed] [Google Scholar]
Позвоночник (Фила Па, 1976)
2001;26:2601–06 [PubMed] [Google Scholar]
31. Дора С., Уолхли Б., Элферинг А. и др.. Значение размеров позвоночного канала в различении симптоматических и бессимптомных грыж диска. Европейский позвоночник J 2002;11:575–81 [PubMed] [Google Scholar]
32. Эдмондстон С.Дж., Сонг С., Брикнелл Р.В. и др. МРТ-оценка сгибания и разгибания поясничного отдела позвоночника у бессимптомных лиц. Мужчина Тер 2000; 5:158–64 [PubMed] [Google Scholar]
33. Эркинтало М.О., Салминен Дж.Дж., Аланен А.М. и др.. Развитие дегенеративных изменений в поясничном межпозвонковом диске: результаты проспективного МРТ-исследования у подростков с болью в пояснице и без нее. Радиология 1995;196:529–33 [PubMed] [Google Scholar]
34.
Фэн Т., Чжао П., Лян Г. Клиническое значение протрузии студенистого ядра: сравнительное исследование 44 пациентов с поясничной протрузией межпозвонкового диска и 73 бессимптомных контролей при трехмерной компьютерной томографии [на китайском языке]. Чжунго Чжун Си И Цзе Хэ Цза Чжи
2000; 20: 347–49.[PubMed] [Google Scholar]
Чжунго Чжун Си И Цзе Хэ Цза Чжи
2000; 20: 347–49.[PubMed] [Google Scholar]
35. Гибсон М.Дж., Шиприт Э.П., Бакли Дж.Х. и др. Магнитно-резонансная томография грыжи диска у подростков. J Bone Joint Surg Br 1987; 69: 699–703 [PubMed] [Google Scholar]
36. Хаманиши С., Кавабата Т., Йоси Т. и др. Узлы Шморля на магнитно-резонансной томографии. Их частота и клиническое значение. Позвоночник (Фила Па, 1976) 1994;19:450–53 [PubMed] [Google Scholar]
37. Healy JF, Healy BB, Wong WH и др. МРТ шейного и поясничного отделов у бессимптомных пожилых спортсменов-мужчин на протяжении всей жизни: частота дегенеративных изменений. J Comput Assist Томогр 1996;20:107–12 [PubMed] [Google Scholar]
38. Jensen MC, Brant-Zawadzki MN, Obuchowski N, et al. Магнитно-резонансная томография поясничного отдела позвоночника у людей без болей в спине. N Engl J Med 1994; 331:69–73 [PubMed] [Google Scholar]
39.
Канаяма М., Тогава Д., Такахаши С. и др.. Поперечное магнитно-резонансное исследование дегенерации поясничного диска у 200 здоровых людей. J Нейрохирург Позвоночник
2009;11:501–07 [PubMed] [Google Scholar]
J Нейрохирург Позвоночник
2009;11:501–07 [PubMed] [Google Scholar]
40. Каракида О., Уэда Х., Уэда М. и др.. Изменения дневного значения Т2 в поясничных межпозвонковых дисках. Клин Радиол 2003;58:389–92 [PubMed] [Google Scholar]
41. Kjaer P, Leboeuf-Yde C, Korsholm L и др. Магнитно-резонансная томография и боль в пояснице у взрослых: диагностическое исследование изображений 40-летних мужчин и женщин. Позвоночник (Фила Па, 1976) 2005; 30:1173–80 [PubMed] [Google Scholar]
42. Kovacs FM, Arana E, Royuela A и др.. Дегенерация диска и хроническая боль в пояснице: связь, которая становится незначительной, если принять во внимание изменения замыкательной пластинки и контур диска. Нейрорадиология 2014; 56:25–33 [PubMed] [Google Scholar]
43. Мацумото М., Окада Э., Тояма Ю. и др. Тандемные возрастные изменения поясничного и шейного межпозвоночных дисков у бессимптомных субъектов. Европейский позвоночник J 2013;22:708–13 [бесплатная статья PMC] [PubMed] [Google Scholar]
44. Пааянен Х., Эркинтало М., Парккола Р. и др.. Возрастная корреляция боли в пояснице и дегенерации поясничного диска. Arch Orthop Trauma Surg
1997; 116:106–07 [PubMed] [Google Scholar]
Пааянен Х., Эркинтало М., Парккола Р. и др.. Возрастная корреляция боли в пояснице и дегенерации поясничного диска. Arch Orthop Trauma Surg
1997; 116:106–07 [PubMed] [Google Scholar]
45. Пааянен Х., Эркинтало М., Куусела Т. и др. Магнитно-резонансное исследование дегенерации диска у молодых пациентов с болью в пояснице. Позвоночник 1989;14:982–85 [PubMed] [Google Scholar]
46. Рэнсон К.А., Керслейк Р.В., Бернетт А.Ф. и др. Магнитно-резонансная томография поясничного отдела позвоночника у бессимптомных профессиональных быстрых боулеров в крикете. J Bone Joint Surg Br 2005; 87:1111–16 [PubMed] [Google Scholar]
47. Сэвидж Р.А., Уайтхаус Г.Х., Робертс Н. Взаимосвязь между магнитно-резонансной томографией поясничного отдела позвоночника и болью в пояснице, возрастом и родом занятий у мужчин. Европейский позвоночник J 1997; 6: 106–14 [бесплатная статья PMC] [PubMed] [Google Scholar]
48.
Silcox DH 3rd, Horton WC, Silverstein AM. МРТ поясничных межпозвонковых дисков: суточные колебания интенсивности сигнала. Позвоночник (Фила Па, 1976)
1995;20:807–11; обсуждение 811–12 [PubMed] [Google Scholar]
Позвоночник (Фила Па, 1976)
1995;20:807–11; обсуждение 811–12 [PubMed] [Google Scholar]
49. Стадник Т.В., Ли Р.Р., Коэн Х.Л. и др.. Кольцевые разрывы и грыжа диска: распространенность и усиление контраста на МРТ-изображениях при отсутствии болей в пояснице или радикулита. Радиология 1998; 206:49–55 [PubMed] [Google Scholar]
50. Szypryt EP, Twining P, Mulholland RC, et al. Распространенность дегенерации диска, связанная с дефектами нервной дуги поясничного отдела позвоночника, оценена с помощью магнитно-резонансной томографии. Позвоночник (Фила Па 1976) 1989;14:977–81 [PubMed] [Google Scholar]
51. Weinreb JC, Wolbarsht LB, Cohen JM и др. Распространенность аномалий пояснично-крестцового межпозвонкового диска на МРТ-изображениях у беременных и бессимптомных небеременных женщин. Радиология 1989;170:125–28 [PubMed] [Google Scholar]
52.
Weishaupt D, Zanetti M, Hodler J и др. МРТ поясничного отдела позвоночника: распространенность экструзии и секвестрации межпозвонкового диска, компрессия нервных корешков, аномалии замыкательной пластинки и остеоартрит фасеточных суставов у бессимптомных добровольцев. Радиология
1998;209:661–66 [PubMed] [Google Scholar]
Радиология
1998;209:661–66 [PubMed] [Google Scholar]
53. Зобель Б.Б., Вадала Г., Дель Весково Р. и др. Количественная оценка ранней дегенерации поясничного межпозвонкового диска у здоровых молодых людей с помощью магнитно-резонансной томографии. Позвоночник (Фила Па, 1976) 2012;37:1224–30 [бесплатная статья PMC] [PubMed] [Google Scholar]
Фрагментация диска при формировании массивных звезд — наблюдения с высоким разрешением в направлении AFGL 2591-VLA 3
A&A 655, A84 (2021)
Фрагментация диска в массивном звездообразовании
Наблюдения с высоким разрешением в направлении AFGL 2591-VLA 3
★ С. Сури 1 , Х. Беутер 1 , К. Гизер 1 , А.1 Ахмади 90 Санчес-Монж 3 , Дж. М. Винтерс 4 , Х. Линц 1 , Th. Henning 1 , M. T. Beltrán 5 , F. Bosco 1 , R. Cesaroni 5 , T. Csengeri 6 , S. Feng 7 ,8 ,9 , M. G. Hoare 10 , К. Г. Джонстон 10 , P. Klaassen 11 , R. Kuiper 12 , 13 , S. Leurini 14 , S. Longmore 15 , S. Lumsden 10 , L. Maud 16 , 10 , L. Maud 16 , 10 , L. Maud 16 , 10 , L. L. Moscadelli 5 , T. Möller 3 , A. Palau 17 , T. Peters 18 , R. E. Pudritz 19 , S. E. Ragan 20 , D. Semenov 1 , 21116, 21116, 21116, 21116, 21116, 21116, 21116, 21116, 21116, 21115 20 , D. Semenov 1 , 21116, 21116, 21115, 21115, 21115 20 . , P. Schilke 3 , J. S. Urquhart 22 , F. Wyrowski 23 и H. Zinnecker 24
Feng 7 ,8 ,9 , M. G. Hoare 10 , К. Г. Джонстон 10 , P. Klaassen 11 , R. Kuiper 12 , 13 , S. Leurini 14 , S. Longmore 15 , S. Lumsden 10 , L. Maud 16 , 10 , L. Maud 16 , 10 , L. Maud 16 , 10 , L. L. Moscadelli 5 , T. Möller 3 , A. Palau 17 , T. Peters 18 , R. E. Pudritz 19 , S. E. Ragan 20 , D. Semenov 1 , 21116, 21116, 21116, 21116, 21116, 21116, 21116, 21116, 21116, 21115 20 , D. Semenov 1 , 21116, 21116, 21115, 21115, 21115 20 . , P. Schilke 3 , J. S. Urquhart 22 , F. Wyrowski 23 и H. Zinnecker 24
1 Институт астрономии Макса Планка,
Кенигштуль 17,
69117
Гейдельберг,
Германия
электронная почта: suemeyye. [email protected]
[email protected]
2 Лейденский университет,
Нильс Борвег 2,
2333
Калифорния
Лейден,
Нидерланды
3 I. Физический институт Кёльнского университета,
Цюльпихер ул. 77,
50937,
Кёльн,
Германия
4 IRAM, 300 rue de la Piscine, Domaine Universitaire,
38406
Сен-Мартен-д’Эр,
Франция
5 INAF, Osservatorio Astrofisico di Arcetri,
Ларго Э. Ферми 5,
50125
Флоренция,
Италия
6 Laboratoire d’astrophysique de Bordeaux, Univ. Бордо, CNRS, B18N, аллея Жоффруа Сент-Илер,
33615
Пессак,
Франция
7 Academia Sinica Институт астрономии и астрофизики,
№1, гл. 4, Рузвельт Роуд,
Тайбэй
10617,
Тайвань,
РПЦ
8 Ключевая лаборатория CAS FAST, Национальная астрономическая обсерватория, Китайская академия наук,
Пекин
100101,
PR Китай
9 Национальная астрономическая обсерватория Японии, Национальные институты естественных наук,
2-21-1 Осава, Митака,
Токио
181-8588,
Япония
10 Школа физики и астрономии Лидского университета,
Лидс
ЛС2 9ДЖТ,
Великобритания
11 Центр астрономических технологий Великобритании, Королевская обсерватория Эдинбурга,
Блэкфорд Хилл,
Эдинбург
ЭХ9 3ХДЖ,
Великобритания
12 Центр астрономии Гейдельбергского университета, Институт теоретической астрофизики,
Альберт-Юберле-Штрассе 2,
69120
Гейдельберг,
Германия
13 Институт астрономии и астрофизики Тюбингенского университета,
Ауф дер Моргенштелле 10,
72076
Тюбинген,
Германия
14 INAF, Osservatorio Astronomico di Cagliari,
Виа делла Сайенца 5,
09047, г. Селаргиус (Калифорния),
Италия
Селаргиус (Калифорния),
Италия
15 Научно-исследовательский институт астрофизики, Ливерпульский университет Джона Мурса,
Ливерпуль,
Л3 5РФ,
Великобритания
16 Европейская южная обсерватория,
Карл-Шварцшильд-ул. 2,
85748
Гархинг,
Германия
17 Институт радиоастрономии и астрофизики (IRyA), UNAM,
Апдо. Почтовый 72-3 (Ксангари), Морелия,
Мичоакан
58089,
Мексика
18 Макс-Планк-Институт астрофизики,
Карл-Шварцшильд-ул. 1,
85748
Гархинг,
Германия
19 Кафедра физики и астрономии Университета Макмастера,
Гамильтон,
Онтарио
Л8С4М1,
Канада
20 Школа физики и астрономии Кардиффского университета,
Здание королевы,
Парад,
Кардифф,
КФ24 3АА,
Великобритания
21 Химический факультет Мюнхенского университета Людвига-Максимилиана,
Бутенандт ул. 5-13, дом Ф,
81377
Мюнхен,
Германия
22 Центр астрофизики и планетологии Кентского университета,
Кентербери,
КТ2,7НХ,
Великобритания
23 Макс-Планк-Институт радиоастрономии (MPIfR),
Ауф дем Хюгель 69,
53121
Бонн,
Германия
24 Автономный университет Чили,
Авда Педро де Вальдивия 425,
Провиденсия,
Сантьяго де Чили,
Чили
Получено:
31
Маршировать
2021
Принято:
14
Август
2021
Аннотация
Контекст. Все больше данных свидетельствует о том, что, как и их маломассивные аналоги, звезды с большой массой формируются в процессе дисковой аккреции. В то же время образование массивных звезд по-прежнему требует высоких скоростей аккреции и, следовательно, высокой плотности газа, что, в свою очередь, может привести к тому, что диски станут неустойчивыми к гравитационной фрагментации.
Все больше данных свидетельствует о том, что, как и их маломассивные аналоги, звезды с большой массой формируются в процессе дисковой аккреции. В то же время образование массивных звезд по-прежнему требует высоких скоростей аккреции и, следовательно, высокой плотности газа, что, в свою очередь, может привести к тому, что диски станут неустойчивыми к гравитационной фрагментации.
Цели. Мы изучаем кинематику и фрагментацию диска вокруг массивной области звездообразования AFGL 2591-VLA 3, которая, как предполагалось, фрагментируется на основании наблюдений, показывающих несколько направлений истечения.
Методы. Мы используем новый набор наблюдений IRAM/NOEMA с высоким разрешением (0».19) на 843 мкм в направлении VLA 3, которые позволяют нам разрешить его диск, охарактеризовать фрагментацию и изучить его кинематику. В дополнение к непрерывному излучению на длине волны 843 мкм наша спектральная установка нацелена на теплый плотный газ и индикаторы истечения, такие как HCN, HC 3 N и SO 2 , а также колебательно-возбужденные линии HCN.
Результаты. Карты континуума и линейного излучения с высоким разрешением показывают множественные фрагменты с субсолнечными массами во внутренней части VLA 3 ~1000 а.е. учился в проекте CORE на 1,37 мм.
Выводы. Мы представляем первое наблюдательное свидетельство фрагментации диска в сторону AFGL 259.1-VLA 3, источник, который считался одним массивным ядром. Хотя сами осколки маломассивны, во вращении диска преобладает протозвезда с массой 10,3 ± 1,8 M ⊙ . Эти данные также показывают, что NOEMA Band 4 может обеспечить максимально достижимое в настоящее время пространственное разрешение на длинах волн (суб) мм при наблюдениях сильных северных источников.
Ключевые слова: звезды: образование / звезды: массивные / методы: интерферометрические
★
Данные NOEMA доступны только в CDS через анонимный ftp cdsarc.u-strasbg.fr (130.79.128.5) или через http://cdsarc. u-strasbg.fr/viz-bin/cat/J /A+A/655/A84
u-strasbg.fr/viz-bin/cat/J /A+A/655/A84
© S. Suri et al. 2021
Статья в открытом доступе, опубликованная EDP Sciences в соответствии с лицензией Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе. , при условии правильного цитирования оригинальной работы.
Финансирование открытого доступа предоставлено Обществом Макса Планка.
1 Введение
Звезды большой массы ( M > 8 M ⊙ ) регулируют динамическую и химическую эволюцию межзвездной среды (МЗС), однако точные пути их образования все еще обсуждаются. Причина, по которой наблюдения за формированием массивных звезд заходят в тупик, двояка. Во-первых, эти объекты встречаются реже, чем их маломассивные аналоги (Крупа, 2002; Чабрие, 2003), и в основном встречаются дальше в плотных скоплениях (например, Циннекер и Йорк, 2007; Беутер и др. , 2007; Тан и др., 2014). Во-вторых, время жизни звезд с большой массой из-за их более высокой светимости короче, потому что они сжигают свое топливо гораздо быстрее. Поскольку они живут короче, их труднее наблюдать на данном этапе. Несмотря на эти трудности, были предприняты огромные наблюдательные и теоретические усилия, направленные на понимание стадий их формирования и эволюции.
, 2007; Тан и др., 2014). Во-вторых, время жизни звезд с большой массой из-за их более высокой светимости короче, потому что они сжигают свое топливо гораздо быстрее. Поскольку они живут короче, их труднее наблюдать на данном этапе. Несмотря на эти трудности, были предприняты огромные наблюдательные и теоретические усилия, направленные на понимание стадий их формирования и эволюции.
В масштабах молекулярных облаков недавняя работа показывает, что фрагментация нитей (например, Кайнулайнен и др., 2017) и массовая аккреция по направлению к сгусткам звездообразования с большой и средней массой (например, Хакар и др., 2018) играют ключевую роль в обеспечении местность, где могут образовываться такие объекты. Когда дело доходит до коллапса отдельных ядер в субпарсековых масштабах, теоретическая работа предсказывает формирование аккреционных дисков вокруг центральных объектов. Важным аспектом формирования массивных звезд является то, что шкала времени Кельвина-Гельмгольца 1 протозвезд намного короче шкалы времени свободного падения их оболочек (например, Палла и Шталер, 1993; Шилке, 2015). Это означает, что у протозвезд с большой массой отсутствует фаза перед главной последовательностью, и вместо этого они зажигают водород, пока еще находятся в фазе аккреции. Из-за радиационного давления, которое возникает на раннем этапе их формирования, то, как звезды с большой массой могут приобретать массы выше 40 90 273 M 90 274 90 283 ⊙ 90 284, долгое время оставалось загадкой (например, Wolfire & Cassinelli 19).87). Однако самые последние исследования показывают, что при наличии аккреционных дисков, подобных дискам маломассивных звезд, и асимметричной аккреции аккреция вещества на ядра с большой массой не затруднена из-за радиационного давления (например, Krumholz et al. и др., 2009; Койпер и др., 2010; Тан и др., 2014; Классен и др., 2016; Койпер и Хосокава, 2018).
Это означает, что у протозвезд с большой массой отсутствует фаза перед главной последовательностью, и вместо этого они зажигают водород, пока еще находятся в фазе аккреции. Из-за радиационного давления, которое возникает на раннем этапе их формирования, то, как звезды с большой массой могут приобретать массы выше 40 90 273 M 90 274 90 283 ⊙ 90 284, долгое время оставалось загадкой (например, Wolfire & Cassinelli 19).87). Однако самые последние исследования показывают, что при наличии аккреционных дисков, подобных дискам маломассивных звезд, и асимметричной аккреции аккреция вещества на ядра с большой массой не затруднена из-за радиационного давления (например, Krumholz et al. и др., 2009; Койпер и др., 2010; Тан и др., 2014; Классен и др., 2016; Койпер и Хосокава, 2018).
Наблюдения за дисками вокруг звезд с большой массой немногочисленны по сравнению с их аналогами с малой и средней массой, что ограничивает нашу способность ограничивать их физические свойства (подробные обзоры см. , например, в Белтране и де Вит, 2016; Чжао и др., 2020). . Однако недавние достижения в области интерферометрии, обеспечивающие разрешение до доли угловой секунды на длинах волн (суб) миллиметров, привели к поворотному моменту в исследованиях звездообразования большой массы, поскольку обнаруживается растущее число дисков вокруг звезд O- и B-типа. (например, Патель и др., 2005; Санчес-Монж и др., 2013; Джонстон и др., 2015, 2020b; Или и др., 2016, 2018; Чесарони и др., 2017; Ченгери и др., 2018; Гинзбург и др., 2018; Жирарт и др., 2018 г. Москаделли и др., 2019 г.; Мод и др. 2019; Аньес-Лопес и др. 2020). Процесс аккреции, опосредованный диском, кажется необходимым для образования объектов с большей массой. Во время этого процесса сами диски могут стать нестабильными из-за их высокой плотности. Диск, подвергающийся кеплеровскому вращению, склонен к фрагментации, когда собственная гравитация и тепловое давление больше не находятся в равновесии (Toomre 1964). Используя трехмерное радиационно-гидродинамическое моделирование (подробное описание моделирования см.
, например, в Белтране и де Вит, 2016; Чжао и др., 2020). . Однако недавние достижения в области интерферометрии, обеспечивающие разрешение до доли угловой секунды на длинах волн (суб) миллиметров, привели к поворотному моменту в исследованиях звездообразования большой массы, поскольку обнаруживается растущее число дисков вокруг звезд O- и B-типа. (например, Патель и др., 2005; Санчес-Монж и др., 2013; Джонстон и др., 2015, 2020b; Или и др., 2016, 2018; Чесарони и др., 2017; Ченгери и др., 2018; Гинзбург и др., 2018; Жирарт и др., 2018 г. Москаделли и др., 2019 г.; Мод и др. 2019; Аньес-Лопес и др. 2020). Процесс аккреции, опосредованный диском, кажется необходимым для образования объектов с большей массой. Во время этого процесса сами диски могут стать нестабильными из-за их высокой плотности. Диск, подвергающийся кеплеровскому вращению, склонен к фрагментации, когда собственная гравитация и тепловое давление больше не находятся в равновесии (Toomre 1964). Используя трехмерное радиационно-гидродинамическое моделирование (подробное описание моделирования см. в Oliva & Kuiper 2020), Ahmadi et al. (2019) изучают фрагментацию массивного диска и «наблюдаемость» такой фрагментации при различных наклонах и расстояниях источника. Это исследование показывает, что неустойчивый по Тумре диск фрагментируется в масштабах ниже 500 а. мсек на расстоянии 800 пк (что соответствует пространственному разрешению ~60 а.е.). Авторы также обнаружили, что фрагменты также могут быть разрешены с помощью IRAM Northern Extended Millimeter Array (NOEMA) с разрешением 0».4, если диск находится под наклоном 10° или 30° при 800 пк. Такая фрагментация диска вокруг звезд с большой массой была обнаружена совсем недавно с помощью наблюдений ALMA с высоким разрешением, выявляющих спиральные структуры внутри диска (Мод и др., 2019).; Джонстон и др. 2020a) и вторичные компоненты (Ilee et al. 2018).
в Oliva & Kuiper 2020), Ahmadi et al. (2019) изучают фрагментацию массивного диска и «наблюдаемость» такой фрагментации при различных наклонах и расстояниях источника. Это исследование показывает, что неустойчивый по Тумре диск фрагментируется в масштабах ниже 500 а. мсек на расстоянии 800 пк (что соответствует пространственному разрешению ~60 а.е.). Авторы также обнаружили, что фрагменты также могут быть разрешены с помощью IRAM Northern Extended Millimeter Array (NOEMA) с разрешением 0».4, если диск находится под наклоном 10° или 30° при 800 пк. Такая фрагментация диска вокруг звезд с большой массой была обнаружена совсем недавно с помощью наблюдений ALMA с высоким разрешением, выявляющих спиральные структуры внутри диска (Мод и др., 2019).; Джонстон и др. 2020a) и вторичные компоненты (Ilee et al. 2018).
Чтобы ответить на открытые вопросы в исследованиях звездообразования большой массы, а именно на лежащие в основе физики и химии при формировании и фрагментации дисков, а также процессы впадения и оттока, мы наблюдали 20 областей звездообразования большой массы (HMSFR) на 1,37 мм в рамках большой программы IRAM NOEMA «CORE 2 » (Beuther et al. 2018). Выборка CORE состоит из северных HMSFR, которые в основном или полностью недоступны для обсерваторий южного полушария (например, ALMA). Программа обеспечивает уникальное понимание физических и химических свойств наблюдаемых регионов, а также подробные тематические исследования (например, Ahmadi et al. 2018; Gieser et al. 2019; Чезарони и др. 2019; Боско и др. 2019; Моттрам и др. 2020; Ольгин и др. 2020 г.) и статистические исследования более крупных выборок (Beuther et al. 2018; Ahmadi, готовится; Gieser et al. 2021). Среди нашей выборки AFGL 2591 является одним из самых ярких HMSFR с L ~ 2 × 10 5 L ⊙ на расстоянии 3,33 кпк (Ригл и др., 2012). Он находится в направлении звездообразующего комплекса Лебедя X и связан с крупномасштабным (>1′ ~ 1 пк), высокоскоростным (Δ V ≥ 30 км с −1 ) молекулярный отток, описанный Bally & Lada (1983). Ранние наблюдения с помощью очень большого массива (VLA) показывают, что AFGL 2591 представляет собой сложное скопление нескольких источников с независимыми областями HII (Кэмпбелл, 1984), с последующими наблюдениями пяти отдельных источников в этом регионе.
2018). Выборка CORE состоит из северных HMSFR, которые в основном или полностью недоступны для обсерваторий южного полушария (например, ALMA). Программа обеспечивает уникальное понимание физических и химических свойств наблюдаемых регионов, а также подробные тематические исследования (например, Ahmadi et al. 2018; Gieser et al. 2019; Чезарони и др. 2019; Боско и др. 2019; Моттрам и др. 2020; Ольгин и др. 2020 г.) и статистические исследования более крупных выборок (Beuther et al. 2018; Ahmadi, готовится; Gieser et al. 2021). Среди нашей выборки AFGL 2591 является одним из самых ярких HMSFR с L ~ 2 × 10 5 L ⊙ на расстоянии 3,33 кпк (Ригл и др., 2012). Он находится в направлении звездообразующего комплекса Лебедя X и связан с крупномасштабным (>1′ ~ 1 пк), высокоскоростным (Δ V ≥ 30 км с −1 ) молекулярный отток, описанный Bally & Lada (1983). Ранние наблюдения с помощью очень большого массива (VLA) показывают, что AFGL 2591 представляет собой сложное скопление нескольких источников с независимыми областями HII (Кэмпбелл, 1984), с последующими наблюдениями пяти отдельных источников в этом регионе. Самый яркий инфракрасный источник, VLA 3, часто называемый самим AFGL 2591, представляет собой горячее ядро, ответственное за конусообразную отражательную туманность, которая видна на изображениях диапазона Gemini K ′ (обзор региона см. в Gieser и др. 2019, их рис. 1). При разрешении 0».4 и размере 1,37 мм VLA 3 наблюдается как одиночное ядро (Беутер и др., 2018) с массой ~40 M ⊙ (Санна и др., 2012). Как упоминалось выше, VLA 3 является частью скопления AFGL 2591 с четырьмя другими источниками, которые выделяются на сантиметровых волнах, а именно областями HII VLA 1 и VLA 2 (Тринидад и др., 2003), звездой типа B9, названной VLA 4, и VLA. 5, который связан с источником инфракрасного излучения (Джонстон и др., 2013 г.).
Самый яркий инфракрасный источник, VLA 3, часто называемый самим AFGL 2591, представляет собой горячее ядро, ответственное за конусообразную отражательную туманность, которая видна на изображениях диапазона Gemini K ′ (обзор региона см. в Gieser и др. 2019, их рис. 1). При разрешении 0».4 и размере 1,37 мм VLA 3 наблюдается как одиночное ядро (Беутер и др., 2018) с массой ~40 M ⊙ (Санна и др., 2012). Как упоминалось выше, VLA 3 является частью скопления AFGL 2591 с четырьмя другими источниками, которые выделяются на сантиметровых волнах, а именно областями HII VLA 1 и VLA 2 (Тринидад и др., 2003), звездой типа B9, названной VLA 4, и VLA. 5, который связан с источником инфракрасного излучения (Джонстон и др., 2013 г.).
Идея, что AFGL 2591-VLA 3, далее для удобства именуемый VLA 3, может быть фрагментированным, что было предложено рядом исследований. В частности, наблюдения мазеров H 2 O с использованием интерферометрии со сверхдлинной базой (РСДБ) в направлении источника выявили существование трех отдельных мазерных скоплений (Санна и др. , 2012). Кроме того, в предыдущем исследовании CORE с использованием выбросов CO, SiO и SO наблюдались несколько направлений оттока. Это указывает либо на дисковый ветер, либо на фрагментацию ниже 1400 а.е., которую наблюдения 1,37 мм не разрешили, при этом каждый фрагмент приводит в действие отдельные потоки (Gieser et al. 2019).).
, 2012). Кроме того, в предыдущем исследовании CORE с использованием выбросов CO, SiO и SO наблюдались несколько направлений оттока. Это указывает либо на дисковый ветер, либо на фрагментацию ниже 1400 а.е., которую наблюдения 1,37 мм не разрешили, при этом каждый фрагмент приводит в действие отдельные потоки (Gieser et al. 2019).).
В этой статье мы представляем новый набор наблюдений NOEMA с высоким пространственным разрешением в качестве расширения большой программы CORE, выполненной на 843 мкм в направлении VLA 3. В спектральную настройку мы включили высоковозбужденные молекулярные линии, чтобы иметь возможность исследовать газовую кинематику в непосредственной близости от протозвезды. Данные показывают фрагментацию в масштабах ~800 а.е. Структура этого исследования такова: мы описываем наблюдения и калибровку данных в разд. 2 и представить анализ карт континуума и линейчатого излучения в разд. 3. Далее следует обсуждение в разд. 4 и резюме наших результатов в разд. 5.
2 Наблюдения
Наблюдения, нацеленные на VLA 3 ( α (J2000) = 20 ч 29 м 24 с . 8, δ (J2000) выполнено с использованием интерферометра IRAM NOEMA в феврале 2018 г. Пять антенн, оснащенных приемником диапазона 4 (275–373 ГГц), использовались в максимально расширенной (A) конфигурации для достижения максимально возможного пространственного разрешения. Частота гетеродина составляла 360,995 ГГц (840 мкм). С помощью нового коррелятора PolyFiX были сняты спектры в диапазоне 353,4–357,1 ГГц со спектральным разрешением 2 МГц, что соответствует разрешению по скорости 1,6 км с 9 .0115 −1 на частоте 356 ГГц. Чтобы получить более высокое спектральное разрешение для выбранного набора сильных линий, мы разместили пять дополнительных спектральных окон (для каждой поляризации) со спектральным разрешением 62,5 кГц (скорость 0,05 км с -1 ). Наблюдения проводились в двухполяризационном и однополосном режимах.
8, δ (J2000) выполнено с использованием интерферометра IRAM NOEMA в феврале 2018 г. Пять антенн, оснащенных приемником диапазона 4 (275–373 ГГц), использовались в максимально расширенной (A) конфигурации для достижения максимально возможного пространственного разрешения. Частота гетеродина составляла 360,995 ГГц (840 мкм). С помощью нового коррелятора PolyFiX были сняты спектры в диапазоне 353,4–357,1 ГГц со спектральным разрешением 2 МГц, что соответствует разрешению по скорости 1,6 км с 9 .0115 −1 на частоте 356 ГГц. Чтобы получить более высокое спектральное разрешение для выбранного набора сильных линий, мы разместили пять дополнительных спектральных окон (для каждой поляризации) со спектральным разрешением 62,5 кГц (скорость 0,05 км с -1 ). Наблюдения проводились в двухполяризационном и однополосном режимах.
Два квазара, 2013 + 370 и 2037 + 511, использовались для амплитудной и фазовой калибровки. Для калибровки полосы пропускания использовался квазар 3C84, а для калибровки абсолютного потока использовалась яркая звезда (MWC349). Погрешность калибровки потока составляет ~20%. Общее время нахождения в источнике составило 7,9 ч с осаждаемым водяным паром (pwv) < 2 мм. Обработка данных была выполнена с использованием калибровки непрерывного и линейного интерферометра 3 (CLIC), части программного обеспечения GILDAS, разработанного Миллиметрическим институтом радиоастрономии (IRAM). Мы извлекли непрерывное излучение 843 мкм из каналов без линий в двух спектральных блоках низкого разрешения (L01 и L02) PolyFiX. Для линий, наблюдаемых с разрешением 2 МГц, непрерывное излучение вычиталось перед визуализацией. Вычитание континуума для линий, охватываемых окнами с высоким спектральным разрешением, было выполнено с использованием метода uv_baseline пакета MAPPING в GILDAS.
Погрешность калибровки потока составляет ~20%. Общее время нахождения в источнике составило 7,9 ч с осаждаемым водяным паром (pwv) < 2 мм. Обработка данных была выполнена с использованием калибровки непрерывного и линейного интерферометра 3 (CLIC), части программного обеспечения GILDAS, разработанного Миллиметрическим институтом радиоастрономии (IRAM). Мы извлекли непрерывное излучение 843 мкм из каналов без линий в двух спектральных блоках низкого разрешения (L01 и L02) PolyFiX. Для линий, наблюдаемых с разрешением 2 МГц, непрерывное излучение вычиталось перед визуализацией. Вычитание континуума для линий, охватываемых окнами с высоким спектральным разрешением, было выполнено с использованием метода uv_baseline пакета MAPPING в GILDAS.
Мы очистили и восстановили каждую отдельную карту с помощью пакета MAPPING GILDAS, где мы использовали алгоритм Кларка. Эмиссия континуума сначала была очищена без клинбокса. Как только мы получили чистую карту континуума, мы использовали чистую рамку вокруг обнаруженного излучения от источника и надежный параметр 0,1 для достижения максимально возможного пространственного разрешения. Мы в интерактивном режиме очищали и повторно устанавливали размер чистого блока после каждого набора итераций, пока очищенный поток как функция идентифицированных чистых компонентов не сойдется. Было показано, что самокалибровка улучшает изображения 1,3 мм полного образца CORE (Beuther et al. 2018). Однако из-за ограниченного отношения сигнал-шум и наличия только 5 антенн в решетке для наблюдений в полосе 4 это не расширило этот набор данных. Поэтому мы не калибровали наши данные самостоятельно. Результирующий размер синтезированного луча составляет 0 дюймов.19× 0′′,17 с позиционным углом 57,9°. Уровень шума в излучении континуума составляет 6,7 мЯн пучок −1 , что было рассчитано в свободной от излучения области.
Мы в интерактивном режиме очищали и повторно устанавливали размер чистого блока после каждого набора итераций, пока очищенный поток как функция идентифицированных чистых компонентов не сойдется. Было показано, что самокалибровка улучшает изображения 1,3 мм полного образца CORE (Beuther et al. 2018). Однако из-за ограниченного отношения сигнал-шум и наличия только 5 антенн в решетке для наблюдений в полосе 4 это не расширило этот набор данных. Поэтому мы не калибровали наши данные самостоятельно. Результирующий размер синтезированного луча составляет 0 дюймов.19× 0′′,17 с позиционным углом 57,9°. Уровень шума в излучении континуума составляет 6,7 мЯн пучок −1 , что было рассчитано в свободной от излучения области.
Мы изобразили линии, используя тот же интерактивный метод очистки, который мы использовали для карты континуума, с той разницей, что чистый блок был установлен на основе интегрированного излучения после каждого набора итераций. Мы выбрали более высокий надежный параметр, 1 (т. е. ближе к естественному взвешиванию), для линейного излучения, поскольку чувствительность для спектральных линий ниже. Это привело к размеру луча 0»,21 × 0»,19с позиционным углом 47,8°. Уровень шума, рассчитанный в безэмиссионном канале, в спектрах низкого и высокого разрешения, снятых с разрешением по скорости 2 и 0,5 км с −1 соответственно, приведен отдельно для каждой карты в табл. 1.
е. ближе к естественному взвешиванию), для линейного излучения, поскольку чувствительность для спектральных линий ниже. Это привело к размеру луча 0»,21 × 0»,19с позиционным углом 47,8°. Уровень шума, рассчитанный в безэмиссионном канале, в спектрах низкого и высокого разрешения, снятых с разрешением по скорости 2 и 0,5 км с −1 соответственно, приведен отдельно для каждой карты в табл. 1.
Таблица 1
Свойства линий, обнаруженных в установке коррелятора 843 мкм.
3 Анализ и результаты
3.1 Излучение в континууме
Наблюдения CORE в направлении VLA 3 на расстоянии 1,37 мм дают представление о химической и физической структуре его оболочки с использованием карт излучения в континууме и линейчатых излучениях с угловым разрешением 0»,4, что соответствует 1400 а.е. на частоте 3,33 кпк (Gieser и др. 2019). На рис. 1 мы показываем излучение континуума 843 мкм, где мы разрешаем диск внутри этой оболочки с угловым разрешением 0»,2 угловых секунды (~ 700 а. е.). Излучение 843 мкм сконцентрировано вблизи центра излучения 1,37 мм и показывает фрагментацию.
е.). Излучение 843 мкм сконцентрировано вблизи центра излучения 1,37 мм и показывает фрагментацию.
Мы идентифицируем два основных ядра, A и B, в центре карты, обнаруженные с достоверностью >5 σ . Морфология излучения континуума 843 мкм имеет вытянутую форму с ядрами A и B, разделенными ~ 800 а.е. Предварительно обнаруживаем (~5 σ ) другое сопутствующее ядро, ядро C, к западу от ядра A. Расстояние между ядром C и ядром A составляет ~ 1400 а.е., аналогично расстоянию между G11.92-0,61 MM1a и MM1b (1920 а. ядра в фрагментированном диске G11.92-0.61 MM 1 (Ilee et al. 2018). Кроме того, на рис. 1 видно, что имеется еще одно ядро 3 σ примерно в 2» северо-западнее ядра A, вблизи контура 5 σ излучения 1,37 мм. Однако мы не включаем это ядро в наш анализ из-за отсутствия уверенности на границе 5 σ контуры излучения 1,37 мм, и его существование остается дискуссионным.
Для ядер, идентифицированных в непрерывном излучении 843 мкм, мы вычисляем массы, используя: (1)
, где S ν — интегрированный поток по ядро, B ν — это функция Planck, расчету для температуры пыли T . расстояние до источника, R – отношение массы газа к пыли, κ ν — непрозрачность пыли при 843 мкм. Из Ossenkopf & Henning (1994) мы интерполируем непрозрачность пыли на 843 мкм и получаем 1,8 см 90 115 2 90 116 г 90 115 -1 90 116 (для плотности 10 90 115 6 90 116 см 90 115 -3 90 116 и пыли с тонкой ледяной мантией). Мы используем массовое отношение газа к пыли, равное 150 (Draine 2011). Распределение температуры AFGL 2591 представлено в Gieser et al. (2019 г., их рис. 4). Мы делаем вывод о средней температуре наших ядер, используя их CH 3 Температурная карта CN равна 200 K. При допущении теплового газопылевого взаимодействия мы используем эту температуру как T d для расчета масс ядра в уравнении. (1). Сумма масс трех идентифицированных ядер составляет ~0,9 M ⊙ . Оценку общей массы, а также индивидуальных масс ядер, представленную в табл. 2, следует принять за нижний предел из-за интерферометрической фильтрации.
расстояние до источника, R – отношение массы газа к пыли, κ ν — непрозрачность пыли при 843 мкм. Из Ossenkopf & Henning (1994) мы интерполируем непрозрачность пыли на 843 мкм и получаем 1,8 см 90 115 2 90 116 г 90 115 -1 90 116 (для плотности 10 90 115 6 90 116 см 90 115 -3 90 116 и пыли с тонкой ледяной мантией). Мы используем массовое отношение газа к пыли, равное 150 (Draine 2011). Распределение температуры AFGL 2591 представлено в Gieser et al. (2019 г., их рис. 4). Мы делаем вывод о средней температуре наших ядер, используя их CH 3 Температурная карта CN равна 200 K. При допущении теплового газопылевого взаимодействия мы используем эту температуру как T d для расчета масс ядра в уравнении. (1). Сумма масс трех идентифицированных ядер составляет ~0,9 M ⊙ . Оценку общей массы, а также индивидуальных масс ядер, представленную в табл. 2, следует принять за нижний предел из-за интерферометрической фильтрации. Основные ошибки в расчетах массы и плотности столба возникают из-за неопределенностей в расстоянии до источника, температуре, соотношении массы газа и пыли и непрозрачности пыли. С учетом этих неопределенностей расчетные массы и плотности столбцов могут различаться в пределах 2−4 раз (также сообщается в Beuther et al. 2018, 2021). Мы оцениваем величину недостающего потока, рассматривая два разных исследования. Во-первых, по сравнению с общим потоком от наших трех ядер (~ 0,1 Ян), общий поток одной тарелки AFGL 2591 на 850 мкм, наблюдаемом с помощью телескопа Джеймса Клерка Максвелла (JCMT), составляет ~8 Ян, что позволяет предположить, что мы отфильтровываем более 95% расширенного излучения (Ди Франческо и др., 2008). Кроме того, Гизер и соавт. (2019) подсчитали, что общая масса в пределах самых внутренних 10 000 а.е. горячего ядра составляет 6,9 M ⊙ . Исходя из этого, мы оцениваем, что наши наблюдения фильтруют около 90% всего потока. Поэтому мы подчеркиваем, что наши наблюдения NOEMA разрешают только внутренний диск AFGL 259.
Основные ошибки в расчетах массы и плотности столба возникают из-за неопределенностей в расстоянии до источника, температуре, соотношении массы газа и пыли и непрозрачности пыли. С учетом этих неопределенностей расчетные массы и плотности столбцов могут различаться в пределах 2−4 раз (также сообщается в Beuther et al. 2018, 2021). Мы оцениваем величину недостающего потока, рассматривая два разных исследования. Во-первых, по сравнению с общим потоком от наших трех ядер (~ 0,1 Ян), общий поток одной тарелки AFGL 2591 на 850 мкм, наблюдаемом с помощью телескопа Джеймса Клерка Максвелла (JCMT), составляет ~8 Ян, что позволяет предположить, что мы отфильтровываем более 95% расширенного излучения (Ди Франческо и др., 2008). Кроме того, Гизер и соавт. (2019) подсчитали, что общая масса в пределах самых внутренних 10 000 а.е. горячего ядра составляет 6,9 M ⊙ . Исходя из этого, мы оцениваем, что наши наблюдения фильтруют около 90% всего потока. Поэтому мы подчеркиваем, что наши наблюдения NOEMA разрешают только внутренний диск AFGL 259. 1, отфильтровывая большую общую оболочку ядер. Отметим также, что при таких высоких температурах непрозрачность тонкой пыли может оказаться недействительной из-за испарения льда с поверхности зерен. Следовательно, если непрозрачность выше принятого значения 1,8 см 2 г −1 , то массы фрагментов, полученные из данных континуума 843 мкм, будут ниже значений, представленных в табл. 2.
1, отфильтровывая большую общую оболочку ядер. Отметим также, что при таких высоких температурах непрозрачность тонкой пыли может оказаться недействительной из-за испарения льда с поверхности зерен. Следовательно, если непрозрачность выше принятого значения 1,8 см 2 г −1 , то массы фрагментов, полученные из данных континуума 843 мкм, будут ниже значений, представленных в табл. 2.
Мы также вычисляем плотности столбцов по направлению к центральным пикам каждого ядра с помощью Хильдебранда (1983): (2)
где — пиковая интенсивность, Ω — телесный угол пучка, μ — средняя молекулярная масса, а m H — масса атома водорода. Мы находим, что плотность столбцов по направлению к центру ядер составляет порядка 10 24 см -2 , что соответствует относительно значительному визуальному поглощению >500 зв. Столбчатые плотности ядер также представлены в таблице 2.
| Рис. 1 Карта плотности потока континуума 843 мкм. |
Таблица 2
Свойства ядер, идентифицированных в континууме 843 мкм.
3.2 Линейное излучение и кинематика
На рис. 2 показан средний спектр, извлеченный из области 0»,7 × 0»,7, покрывающей идентифицированные ядра. Вращательный и роколебательный переходы HCN ответственны за самые яркие линии в спектре 843 мкм. HCN становится наиболее распространенным N-содержащим веществом при температурах выше ~200 К, когда водяной лед испаряется. Это связано с химическими реакциями, в которых участвуют OH, N, N 2 и углеводороды. OH образуется из H 2 O высокоэнергетическими процессами, а N образуется при разрушении N 2 He + . Затем OH быстро реагирует с N, что приводит к NO, который реагирует с углеводородами и образует HCN. Ключевые реакции этой химии имеют барьеры и требуют температуры 100–200 К для активации. Эта высокотемпературная химия хорошо изучена как теоретически, так и экспериментально (например, Rodgers & Charnley 2001; Feng et al. 2015). В дополнение к этому мы обнаруживаем множественные переходы SO 2 , HC 3 N и HCO + линий.
2 показан средний спектр, извлеченный из области 0»,7 × 0»,7, покрывающей идентифицированные ядра. Вращательный и роколебательный переходы HCN ответственны за самые яркие линии в спектре 843 мкм. HCN становится наиболее распространенным N-содержащим веществом при температурах выше ~200 К, когда водяной лед испаряется. Это связано с химическими реакциями, в которых участвуют OH, N, N 2 и углеводороды. OH образуется из H 2 O высокоэнергетическими процессами, а N образуется при разрушении N 2 He + . Затем OH быстро реагирует с N, что приводит к NO, который реагирует с углеводородами и образует HCN. Ключевые реакции этой химии имеют барьеры и требуют температуры 100–200 К для активации. Эта высокотемпературная химия хорошо изучена как теоретически, так и экспериментально (например, Rodgers & Charnley 2001; Feng et al. 2015). В дополнение к этому мы обнаруживаем множественные переходы SO 2 , HC 3 N и HCO + линий. Лед SO 2 испаряется и становится очень обильным в газовой фазе при температурах выше ~70 K, в температурном режиме около линии снега воды (Sandford & Allamandola 1993). Среди всех в абсорбции обнаружен только переход HCO + (4–3). Вероятно, это связано с наличием холодного газа HCO + в выделенной холодной внешней оболочке, которая является разбавленной и, следовательно, более ионизированной, чем внутренний диск. Согласно Ширли (2015), эффективная плотность для возбуждения линии 1 К HCO + (4–3) (для Т кин = 50 К) составляет 7,2 × 10 3 см −3 . Если оболочка вокруг VLA 3 содержит некоторый расширенный объем, где плотность порядка <10 4 см −3 , а температура все еще повышена и >40 К, то предположение о расширенном HCO + , которое приводит к такому линия поглощения может стать действительной. Однако, поскольку мы отфильтровываем большую часть расширенного излучения, мы не можем исключить возможность того, что особенность поглощения может быть артефактом изображения.
Лед SO 2 испаряется и становится очень обильным в газовой фазе при температурах выше ~70 K, в температурном режиме около линии снега воды (Sandford & Allamandola 1993). Среди всех в абсорбции обнаружен только переход HCO + (4–3). Вероятно, это связано с наличием холодного газа HCO + в выделенной холодной внешней оболочке, которая является разбавленной и, следовательно, более ионизированной, чем внутренний диск. Согласно Ширли (2015), эффективная плотность для возбуждения линии 1 К HCO + (4–3) (для Т кин = 50 К) составляет 7,2 × 10 3 см −3 . Если оболочка вокруг VLA 3 содержит некоторый расширенный объем, где плотность порядка <10 4 см −3 , а температура все еще повышена и >40 К, то предположение о расширенном HCO + , которое приводит к такому линия поглощения может стать действительной. Однако, поскольку мы отфильтровываем большую часть расширенного излучения, мы не можем исключить возможность того, что особенность поглощения может быть артефактом изображения. ОХС 9Линия поглощения 0115 + (4–3) смешивается с соседней эмиссионной линией SO 2 и не разрешается в спектре низкого спектрального разрешения. Полный список обнаруженных молекул и их переходные свойства представлены в табл. критические плотности более 10 10 см −3 исследуют теплый и плотный материал в непосредственной близости от протозвезды. Мы также обнаруживаем более высокое возбуждение v 2 = 2 излучение в сторону VLA 3. Однако эти линии имеют гораздо более низкое отношение сигнал/шум (~5) и, следовательно, их трудно отобразить. Эти линии ранее были обнаружены в направлении AFGL 2591 с помощью субмиллиметровой матрицы (SMA), однако из-за более низкого углового разрешения этих данных структура внутренних нескольких тысяч а.е. диска AFGL 2591 осталась неразрешенной (Benz et al. 2007; Вич и др., 2013).
ОХС 9Линия поглощения 0115 + (4–3) смешивается с соседней эмиссионной линией SO 2 и не разрешается в спектре низкого спектрального разрешения. Полный список обнаруженных молекул и их переходные свойства представлены в табл. критические плотности более 10 10 см −3 исследуют теплый и плотный материал в непосредственной близости от протозвезды. Мы также обнаруживаем более высокое возбуждение v 2 = 2 излучение в сторону VLA 3. Однако эти линии имеют гораздо более низкое отношение сигнал/шум (~5) и, следовательно, их трудно отобразить. Эти линии ранее были обнаружены в направлении AFGL 2591 с помощью субмиллиметровой матрицы (SMA), однако из-за более низкого углового разрешения этих данных структура внутренних нескольких тысяч а.е. диска AFGL 2591 осталась неразрешенной (Benz et al. 2007; Вич и др., 2013).
Для дальнейшего анализа мы используем наиболее заметные линии в нашем наборе данных: HCN (4–3), HCN (4–3) v 2 = 1 (оба l = 1e и l = 1f), HC 3 N (39–38) и SO 2 (12 4,8 –12 3,9283 ). На рис. 3 более подробно показано линейное излучение по направлению к центру каждой сердцевины, усредненное по размеру луча. Отметим, что среди этих переходов высокое отношение сигнал/шум ровибрационных линий HCN позволило получить изображение с более высоким разрешением по скорости 0,5 км с −1 по сравнению с остальными линиями, представленными на рис. 3. , полученные с разрешением по скорости 2 км с −1 . Переход l = 1f колебательно-возбужденного HCN является самым сильным, достигая пиковой яркости 100 К по направлению к ядру А и 60 К по направлению к ядру В. линия 30 К (Бенц и др., 2007) и 15 К (Вич и др., 2013), наблюдаемая с более низким угловым разрешением 0»,6 и 3»,4 × 2»,0. Линия HCN в основном состоянии является самой широкой и показывает провал на скорости источника по направлению к ядрам A и B, что указывает на оптически толстое излучение. Он также перекошен и более растянут в сторону красных смещенных скоростей, которые могут быть связаны с протозвездным истечением.
На рис. 3 более подробно показано линейное излучение по направлению к центру каждой сердцевины, усредненное по размеру луча. Отметим, что среди этих переходов высокое отношение сигнал/шум ровибрационных линий HCN позволило получить изображение с более высоким разрешением по скорости 0,5 км с −1 по сравнению с остальными линиями, представленными на рис. 3. , полученные с разрешением по скорости 2 км с −1 . Переход l = 1f колебательно-возбужденного HCN является самым сильным, достигая пиковой яркости 100 К по направлению к ядру А и 60 К по направлению к ядру В. линия 30 К (Бенц и др., 2007) и 15 К (Вич и др., 2013), наблюдаемая с более низким угловым разрешением 0»,6 и 3»,4 × 2»,0. Линия HCN в основном состоянии является самой широкой и показывает провал на скорости источника по направлению к ядрам A и B, что указывает на оптически толстое излучение. Он также перекошен и более растянут в сторону красных смещенных скоростей, которые могут быть связаны с протозвездным истечением. В отличие от ядер A и B, мы не обнаруживаем колебательно-возбужденную эмиссию HCN по направлению к ядру C. Интересно, что эмиссия HCN в основном состоянии и SO 9Излучения 0283 2 в направлении ядра C имеют одинаковую яркость, в отличие от ядер A и B с излучением HCN, которое меньше самопоглощается на этом луче зрения из-за более низкой плотности столбцов.
В отличие от ядер A и B, мы не обнаруживаем колебательно-возбужденную эмиссию HCN по направлению к ядру C. Интересно, что эмиссия HCN в основном состоянии и SO 9Излучения 0283 2 в направлении ядра C имеют одинаковую яркость, в отличие от ядер A и B с излучением HCN, которое меньше самопоглощается на этом луче зрения из-за более низкой плотности столбцов.
Мы представляем карты моментов (интегральная интенсивность, взвешенная по интенсивности пиковая скорость и ширина линии скорости) пяти выбранных переходов на рис. 4. Все линии HCN показывают протяженную морфологию источника в направлении север-юг, с Эмиссия линии HCN в основном состоянии простирается также в направлении восток-запад к ядру C. Интегральная эмиссия между −10 и ~1 км с −1 колебательно-возбужденных переходов пиков HCN между ядрами A и B, хотя карты их каналов показывают, что эти два ядра можно идентифицировать по отдельности (см. рис. A.1 и A.2). Эмиссия SO 2 имеет широкое распространение, охватывая все три ядра, а также простирается к северу и северо-востоку от ядра А. Такое поведение свидетельствует о том, что ядро А и его ближайшие окрестности подвержены толчкам. Интегрированные пики эмиссии HC 3 N вблизи ядра A, яркие в направлении ядра B, но не обнаружены в направлении ядра C. Пространственное распределение HC 3 Эмиссия N по сравнению с непрерывной эмиссией 1,3 мм в направлении VLA 3 подробно обсуждается Jiménez-Serra et al. (2012), наблюдения с использованием SMA с разрешением 0».5. Наши наблюдения с более высоким разрешением подтверждают двухпиковый характер излучения (см. рис. A.5), несмотря на то, что интегрированное излучение наиболее яркое между ядрами A и B.
Такое поведение свидетельствует о том, что ядро А и его ближайшие окрестности подвержены толчкам. Интегрированные пики эмиссии HC 3 N вблизи ядра A, яркие в направлении ядра B, но не обнаружены в направлении ядра C. Пространственное распределение HC 3 Эмиссия N по сравнению с непрерывной эмиссией 1,3 мм в направлении VLA 3 подробно обсуждается Jiménez-Serra et al. (2012), наблюдения с использованием SMA с разрешением 0».5. Наши наблюдения с более высоким разрешением подтверждают двухпиковый характер излучения (см. рис. A.5), несмотря на то, что интегрированное излучение наиболее яркое между ядрами A и B.
Все карты пиковых скоростей, представленные на рис. 4, за исключением излучение HCN (4–3) в основном состоянии показывает глобальный градиент скорости с северо-востока на юго-запад (от синего к красному). Скоростная структура излучения HCN(4–3) достаточно сложна, так как вблизи скорости источника (см. рис. 3) она уплощается, а к ядрам А и В самопоглощается. точно вытекает из этого перехода. В более крупном масштабе CH 3 Эмиссия CN, наблюдаемая на 1,37 мм в рамках наблюдений CORE с более низким угловым разрешением, показывает аналогичный сине-красный градиент скорости в направлении AFGL 2591, согласующийся с нашими наблюдениями (Ahmadi et al., в процессе подготовки). Сходство подразумевает, что градиент скорости теплого и плотного газа, который мы наблюдаем в масштабе ~2000 а.е., может быть унаследован от движений газа большего масштаба.
точно вытекает из этого перехода. В более крупном масштабе CH 3 Эмиссия CN, наблюдаемая на 1,37 мм в рамках наблюдений CORE с более низким угловым разрешением, показывает аналогичный сине-красный градиент скорости в направлении AFGL 2591, согласующийся с нашими наблюдениями (Ahmadi et al., в процессе подготовки). Сходство подразумевает, что градиент скорости теплого и плотного газа, который мы наблюдаем в масштабе ~2000 а.е., может быть унаследован от движений газа большего масштаба.
На рис. 4 видно, что дисперсия скоростей увеличивается в направлении расположения ядер. Как также видно из спектров, показанных для каждого отдельного ядра на рис. 3, вращательная линия основного состояния HCN (4–3) имеет большую ширину. Широкая SO 2 ширины линий простираются дальше к северу от ядер A и B, тогда как эмиссия HC 3 N показывает, что наибольшая ширина линий находится между ядрами A и B, а также между ядрами B и C, хотя само ядро C не обнаружено в HC . 3 Н эмиссия.
3 Н эмиссия.
| Рис. 2 Верхняя панель: спектр низкого спектрального разрешения , пространственно усредненный по области 0′′,7 × 0′′,7 с центром в точке α = 20 ч 29 м 24 с .876, δ = +40°11′19′′.216, охватывающий ядра A, B, C. Средняя панель : увеличение диапазона частот от 354,2 до 355,3 ГГц. Нижняя панель : увеличение диапазона частот от 356,4 до 357,1 ГГц. Горизонтальная серая пунктирная линия соответствует уровню отношения сигнал/шум 5 σ ( σ = 3,4 мЯн луч −1 ). |
| Рис. 3 Спектры пяти наиболее заметных переходов к центру ядер A ( , верхняя панель ), B (, средняя панель ) и C (, нижняя панель ), усредненные по размеру балки. Вертикальная серая пунктирная линия указывает скорость источника. |
Рис. 4 4Карты моментов пяти наиболее заметных линий в наших наблюдениях. Каждая строка представляет собой линию, а столбцы слева направо показывают интегрированную интенсивность, скорость, взвешенную по интенсивности, и карты дисперсии скорости. Контуры в каждой подпанели обозначают 3, 5, 6 и 7 σ уровни излучения непрерывного излучения 843 мкм. Размер луча наблюдений показан в правом нижнем углу каждой подпанели. Скорость источника составляет −5,5 км с −1 . |
| Рис. 5 Левая панель : взвешенная по интенсивности карта пиковой скорости усредненного колебательно-возбужденного излучения HCN. Черными контурами отмечена эмиссия континуума 3, 5, 6 и 7 σ 843 мкм. Стрелки показывают направление крупномасштабного оттока с востока на запад, наблюдаемого в выбросе CO(2−1), синим и красным цветами показаны линейные выбросы с синим и красным смещением (см. Gieser et al. 2019).). Правая панель : PV-диаграмма для усредненной колебательно-возбужденной эмиссии HCN, извлеченная из среза вдоль пунктирной линии, показанной на левой панели. |
4 Обсуждение
4.1 Фрагментация диска и кинематика
Численные модели формирования диска (например, Oliva & Kuiper 2020) предсказывают фрагментацию диска и образование звезд-компаньонов и спиралевидных структур. Синтетические наблюдения, созданные с использованием этих (Ахмади и др., 2019 г.) и других моделей (Янкович и др., 2019 г.), предсказывают, что подструктуры дисков можно наблюдать с помощью таких интерферометров, как ALMA и NOEMA. В моделях, обсуждаемых Ahmadi et al. (2019), гравитационно неустойчивый диск фрагментируется и образует несколько ядер-компаньонов, находящихся в гидростатическом равновесии внутри диска, где каждое ядро образует свой собственный диск. В наших наблюдениях мы обнаруживаем один фрагментированный диск с тремя ядрами-компаньонами на расстоянии 800 и 1400 а.е.
В наших наблюдениях мы обнаруживаем один фрагментированный диск с тремя ядрами-компаньонами на расстоянии 800 и 1400 а.е.
Аналогичным наблюдаемым примером фрагментации диска размером 1000 а.е. является AFGL 4176 (Johnston et al. 2020a). В своем более раннем исследовании с низким разрешением (Джонстон и др., 2015) авторы сообщают о неразрешенной большой структуре с кеплеровским вращением. Однако их наблюдения с более высоким разрешением (30 мсек. дуги, Джонстон и др., 2020a) показывают, что диск фрагментирован в спираль и нестабилен по Тумре. Восточный спиральный рукав также показывает конденсацию, отстоящую примерно на 700 а.0003
Колебательно-возбужденные линии HCN являются хорошими инструментами для исследования горячего плотного газа вблизи протозвезд, а энергетические уровни двух колебательно-возбужденных переходов HCN, которые мы наблюдали, очень близки (~1060 К, см. Таблицу 1), что позволяет нам усреднить эти линии и изучить кинематику диска с меньшим уровнем шума (~30 мЯн луч −1 ). На рис. 5 мы представляем полученную взвешенную по интенсивности карту пиковой скорости усредненных линий HCN, v 2 = 1, l = 1e и v 2 = 1, l = 1f и диаграмма положение-скорость (PV), полученная вдоль градиента скорости северо-восток-юго-запад.
На рис. 5 мы представляем полученную взвешенную по интенсивности карту пиковой скорости усредненных линий HCN, v 2 = 1, l = 1e и v 2 = 1, l = 1f и диаграмма положение-скорость (PV), полученная вдоль градиента скорости северо-восток-юго-запад.
Чтобы оценить кинематическую массу протозвезды, мы подогнали кеплеровские кривые вращения к диаграмме PV, используя общедоступный пакет Python KeplerFit 4 , разработанный Bosco et al. (2019). KeplerFit использует метод, разработанный Seifried et al. (2016), который оценивает самые экстремальные скорости в каждой радиальной позиции от протозвезды, а затем подгоняет кеплеровский профиль скорости к извлеченным точкам данных PV. Чтобы предотвратить подгонку неразрешенного излучения, которое часто приводит к плоским профилям скорости, мы воздерживаемся от подгонки скоростей, близких к протозвезде, поэтому исключаем из подгонки внутренние 700 а.е. (~ один размер луча). Подгоняя остальные скорости к 5 σ эмиссионный уровень, мы заключаем массу заключенного в 10,3 ± 1,8 M ⊙ . Процедура KeplerFit предполагает наклон 90°, и поскольку мы наблюдаем только часть скорости вращения (пропорциональную sin 2 ( i ), где i — наклон), оценки массы всегда являются нижним пределом ( см. уравнение (A.3) в Bosco et al., 2019). Приведенное значение х 2 для кеплеровской подгонки равно 0,47. Это ниже ожидаемого значения 1 для хорошей подгонки, однако, основываясь на предыдущих исследованиях (например, Wang et al. 2012), мы знаем, что AFGL 2591 диск не находится в идеальном кеплеровом вращении.
Процедура KeplerFit предполагает наклон 90°, и поскольку мы наблюдаем только часть скорости вращения (пропорциональную sin 2 ( i ), где i — наклон), оценки массы всегда являются нижним пределом ( см. уравнение (A.3) в Bosco et al., 2019). Приведенное значение х 2 для кеплеровской подгонки равно 0,47. Это ниже ожидаемого значения 1 для хорошей подгонки, однако, основываясь на предыдущих исследованиях (например, Wang et al. 2012), мы знаем, что AFGL 2591 диск не находится в идеальном кеплеровом вращении.
Основываясь на оценках потери массы на расстоянии 1,3 см и ИК-светимости региона, Санна и др. (2012) оценивают массу VLA 3 в диапазоне 20−38 M ⊙ . Есть несколько причин несоответствия между этими более высокими массами для региона и замкнутой массой, которую мы рассчитали, предполагая кеплеровский диск, отслеживаемый колебательно возбужденным излучением HCN. Ранее, используя наблюдения HDO и HO с разрешением 0». 5, Wang et al. (2012) показывают, что градиент скорости с северо-востока на юго-запад представляет собой комбинацию субкеплеровского вращения и хаббловского расширения, вероятно, вызванного массивным истечением и звездным ветром. Также вероятно, что существует большое количество массы за пределами области, которую вибрационно возбужденное излучение HCN отслеживает или отфильтровывает интерферометрическими наблюдениями, что может повлиять на профиль вращения диска. Кроме того, если аккреция все еще продолжается, то полная светимость представляет собой сумму собственной светимости протозвезды и аккреционной светимости. Следовательно, массу, рассчитанную на основе динамической подгонки, следует строго сравнивать с массой, полученной из собственной светимости VLA 3.
5, Wang et al. (2012) показывают, что градиент скорости с северо-востока на юго-запад представляет собой комбинацию субкеплеровского вращения и хаббловского расширения, вероятно, вызванного массивным истечением и звездным ветром. Также вероятно, что существует большое количество массы за пределами области, которую вибрационно возбужденное излучение HCN отслеживает или отфильтровывает интерферометрическими наблюдениями, что может повлиять на профиль вращения диска. Кроме того, если аккреция все еще продолжается, то полная светимость представляет собой сумму собственной светимости протозвезды и аккреционной светимости. Следовательно, массу, рассчитанную на основе динамической подгонки, следует строго сравнивать с массой, полученной из собственной светимости VLA 3.
| Рис. 6 Карта Toomre Q взята из Ahmadi et al. (в подготовке) с наложенными белыми контурами континуума 843 мкм (3, 5, 6 и 7 σ ) и местоположениями водного мазера из Санны и др. |
4.2. Пространственно совпадающее мазерное излучение
H 2 O мазеры обычно считаются указателями активного звездообразования, когда мазинг происходит в условиях высокой плотности (> 10 8 см −3 ) и температур (>400 K) ( Элицур и др., 1989). Эти условия могут выполняться в протозвездных дисках, а также в ударном газе за счет, например, оттоки (например, Uscanga et al. 2010). В случае VLA 3 Санна и соавт. (2012) представляют подробное исследование кинематики H 2 Мазеры O, использующие многоэпохальные наблюдения массива очень длинных базовых линий (VLBA). Они обнаружили, что мазерное излучение воды пространственно распределено в трех кластерах в пределах 2000 а.е. области. Чтобы исследовать расположение этих мазерных скоплений по отношению к фрагментам, которые мы обнаруживаем в этом исследовании, и стабильности диска VLA 3, на рис. 6 мы представляем карту Toomre Q , наложенную на излучение континуума 843 мкм и Мазерные локации. Карта Toomre Q получена как часть выборочного исследования кинематики и стабильности источников CORE при излучении 1,37 мм (Ahmadi et al., в процессе подготовки). Для АФГЛ 2591 авторы используют температуры, полученные по эмиссии CH 3 CN ( T медиана ~ 130 K), и предполагают звезду 16 M ⊙ в центре. Предполагаемая масса 16 M ⊙ получена из кеплеровской аппроксимации диаграммы CH 3 CN PV. Это значение больше, чем кинематическая масса, полученная из наших наблюдений 843 мкм, однако, как упоминалось выше, излучение 1,37 мм следует за расширенным излучением, которое отфильтровано на картах 843 мкм, следовательно, большая заключенная масса.
Они обнаружили, что мазерное излучение воды пространственно распределено в трех кластерах в пределах 2000 а.е. области. Чтобы исследовать расположение этих мазерных скоплений по отношению к фрагментам, которые мы обнаруживаем в этом исследовании, и стабильности диска VLA 3, на рис. 6 мы представляем карту Toomre Q , наложенную на излучение континуума 843 мкм и Мазерные локации. Карта Toomre Q получена как часть выборочного исследования кинематики и стабильности источников CORE при излучении 1,37 мм (Ahmadi et al., в процессе подготовки). Для АФГЛ 2591 авторы используют температуры, полученные по эмиссии CH 3 CN ( T медиана ~ 130 K), и предполагают звезду 16 M ⊙ в центре. Предполагаемая масса 16 M ⊙ получена из кеплеровской аппроксимации диаграммы CH 3 CN PV. Это значение больше, чем кинематическая масса, полученная из наших наблюдений 843 мкм, однако, как упоминалось выше, излучение 1,37 мм следует за расширенным излучением, которое отфильтровано на картах 843 мкм, следовательно, большая заключенная масса. Как видно на рисунке, диск нестабилен ( Q < 2) в значительной степени за исключением непосредственного окружения ядра A.
Как видно на рисунке, диск нестабилен ( Q < 2) в значительной степени за исключением непосредственного окружения ядра A.
Мазерное излучение скопления SE совпадает с континуальным пиком ядра A в пределах ~0′′.1. Хотя мы не наблюдаем ядер континуума в точном местоположении скоплений MW или NE, существует эмиссия SO 2 , простирающаяся за пределы ядра A по направлению к скоплению NE (см. рис. 4, нижняя панель). Действительно, ширина линии скорости SO 2 в этом месте широкая (~6 км с −1 ), что соответствует сценарию, предложенному Санной и др. (2012), что северо-восточное скопление связано с молодой протозвездой по имени VLA 3-N к северу от нашего ядра A. Скорость выброса теплого плотного газа, наблюдаемого в направлении северо-восточного скопления, между −9и − 7 км с −1 , согласуется со скоростями мазерного излучения в скоплении, подтверждая физическую связь между наблюдаемым теплым плотным газом и мазерным излучением.
Расположение ядра C, прямо вдоль оси, перпендикулярной главной оси вращения диска, и между мазерными скоплениями SE и MW, намекает на другую возможность происхождения этого ядра. Наряду с его связью с необычно широкой эмиссией HCN (~20 км с −1 , см. рис. 4) и протяженным SO 9Эмиссия 0283 2 в том же направлении в диапазоне от −4 до −6 км с −1 , согласующаяся со скоростями скопления MW, позволяет предположить, что ядро C может быть частью восточно-западного истечения.
Наряду с его связью с необычно широкой эмиссией HCN (~20 км с −1 , см. рис. 4) и протяженным SO 9Эмиссия 0283 2 в том же направлении в диапазоне от −4 до −6 км с −1 , согласующаяся со скоростями скопления MW, позволяет предположить, что ядро C может быть частью восточно-западного истечения.
Альтернативный сценарий о природе ядер A и B возникает, когда мы рассматриваем юго-восточное мазерное скопление и радиоконтинуум (Санна и др., 2012) как отслеживающие положение протозвезды в VLA 3 между ядрами A и B , В этом случае излучение континуума 843 мкм может следовать по двум краям диска, при этом центр диска (рядом с протозвездой) ослабляется полостью оттока, которая видна в ближнем ИК-излучении (Джонстон и др., 2013). . Однако мы знаем, что Toomre 9Значения 0273 Q уменьшаются по направлению к ядру B, что делает маловероятным наличие гладкого нефрагментированного диска вокруг протозвезды. Эмиссия 3 σ вокруг ядер A и B также демонстрирует дополнительную субструктуру, подтверждающую сценарий, в котором диск фрагментирован.
4.3 Диск против фрагментации ядра
Ряд различных механизмов, а именно термическая (Джинс) или турбулентная фрагментация ядер и волокон (например, Inutsuka & Miyama 1997; Padoan & Nordlund 2002) и фрагментация диска (например, Matsumoto & Hanawa 2003; Kratter & Lodato 2016; Meyer et al. 2017, 2018; Oliva & Kuiper 2020), как полагают, играют роль на разных уровнях при формировании множественных систем и кластеров. Используя наблюдения VLA с высоким разрешением, Tobin et al. (2016) характеризуют множественность протозвезд в маломассивной области звездообразования молекулярного облака Персея и обнаруживают, что сценарий фрагментации диска предпочтительнее для расстояний ≤300 а.е. Для масштабов выше 1000 а.е. они обнаружили, что доминирующим механизмом является фрагментация ядра (термальная или турбулентная). В режиме средней массы Palau et al. (2018) представляют исследование фрагментации ALMA, достигающее пространственного разрешения 100 а. более крупные масштабы 0,1 пк (аналогично, например, Palau et al. 2015; Beuther et al. 2018).
2015; Beuther et al. 2018).
Фрагментация в режиме большой массы ниже 1000 а. Первоначальные наблюдения CORE VLA 3 выявили 3 ядра при непрерывном излучении 1,37 мм со средним расстоянием ~15 000 а.е. (Беутер и др., 2018). Это исследование показывает, что свойства фрагментации (среднее расстояние и масса фрагментов) согласуются с фрагментацией термических Джинсов, о чем также сообщалось в предыдущих исследованиях (например, Gutermuth et al. 2011; Palau et al. 2015). С текущими наблюдениями 843 мкм мы теперь рассматриваем масштабы намного ниже фрагментации ядра (<1000 а.е.), где гравитационные нестабильности в протозвездных дисках играют жизненно важную роль. Используя плотность ( n = 10 7 см −3 ) и значения температуры ( T = 250 K) для AFGL 2591 на ~ 1000 а.е., указанные в Palau et al. (2014), в соответствии с Gieser et al. (2021), мы получаем массу Джинса ~6 M ⊙ и длину Джинса ~7000 а.е. И массы ядра, и расстояния, которые мы вычисляем из эмиссии континуума 843 мкм, на порядок ниже, чем мы ожидаем от фрагментации родительского ядра в масштабе 1000 а. е., и, следовательно, несовместимы со сценарием фрагментации Джинса. Наши фрагменты, расположенные в нестабильном диске Тоомре VLA 3, разделенные ~800 а.е., предполагают фрагментацию диска ниже 1000 а.е. Однако мы признаем, что Toomre 9Карта 0273 Q создана в предположении кеплеровского вращения, которое в случае VLA 3 оказалось более сложной картиной из-за массивного оттока, питаемого протозвездой (Ванг и др., 2012).
е., и, следовательно, несовместимы со сценарием фрагментации Джинса. Наши фрагменты, расположенные в нестабильном диске Тоомре VLA 3, разделенные ~800 а.е., предполагают фрагментацию диска ниже 1000 а.е. Однако мы признаем, что Toomre 9Карта 0273 Q создана в предположении кеплеровского вращения, которое в случае VLA 3 оказалось более сложной картиной из-за массивного оттока, питаемого протозвездой (Ванг и др., 2012).
5 Резюме
Мы представили наблюдения NOEMA с высоким угловым разрешением (0».19 или ~700 а.е.) в направлении AFGL 2591-VLA 3, проведенные с новым высокочастотным диапазоном (полоса 4) на 843 мкм. Наблюдения впервые показывают фрагментацию ниже ~1000 а.е. в направлении AFGL 259.1-ВЛА 3 горячая активная зона. Мы идентифицировали три отдельных маломассивных ядра (<1 M ⊙ ): A, B и C. Ядро C предварительно обнаружено в эмиссии континуума с уровнем достоверности 5 σ , но заметно в HCN(4– 3) вращательное основное состояние и излучение линии SO 2 .
Наши данные об излучении линии указывают на вращающуюся дискообразную структуру с градиентом скорости с северо-востока на юго-запад. Предполагая кеплеровское вращение диска, мы получаем кинематическую массу 10,3 ± 1,8 М ⊙ . Этот градиент скорости с аналогичной осью вращения также виден в предыдущих наблюдениях NOEMA на 1,37 мм, где восстановлена более крупная структура (Ahmadi et al., в процессе подготовки), предполагая, что кинематика внутреннего диска, разрешенная в этом исследовании на 843 мкм, унаследованы от крупномасштабных движений газа.
Расположение ядер B и C согласуется с низкими значениями Toomre Q по всему диску, который в значительной степени неустойчив к гравитационной фрагментации (Ahmadi et al., в процессе подготовки). Мы находим, что скорости H 2 Мазерные скопления O NE и MW согласуются со скоростями линейчатого излучения в наших наблюдениях. В частности, мы наблюдаем широкое излучение SO 2 и эмиссию HCN, указывающую на до- или протозвездную активность, в направлении расположения этих скоплений с их лучевыми скоростями в диапазоне от −2 км с −1 до −10 км с . −1 .
−1 .
Наши результаты подтверждают сценарий формирования массивных объектов в результате аккреции диска, когда сам диск может фрагментироваться, образуя сопутствующие ядра. Будущие наблюдения с более высокой чувствительностью дадут представление о том, сформировали ли идентифицированные ядра в основном протозвездном диске свои собственные диски, как это было предсказано в недавней теоретической работе.
Благодарности
Мы благодарим анонимного рецензента за их время и ценные комментарии, которые улучшили эту рукопись. Эта работа основана на наблюдениях, проведенных в рамках проекта L14AB с помощью интерферометра IRAM NOEMA. IRAM поддерживается INSU/CNRS (Франция), MPG (Германия) и IGN (Испания). Авторы благодарят Альберто Санну за информацию о местонахождении водных мазеров. С.С. и Х.Б. выражаем признательность Европейскому исследовательскому совету за поддержку в рамках рамочной программы Horizon 2020 посредством гранта консолидатора ERC CSF-648405. КАК М. поддерживается Центром совместных исследований 956, подпроект A6, финансируемый Deutsche Forschungsgemeinschaft (DFG), идентификатор проекта 184018867. Р.К. признает финансовую поддержку через исследовательские гранты Emmy Noether и Heisenberg, финансируемые Немецким исследовательским фондом (DFG) в рамках гранта №. КУ 2849/3 и 2849/9. AP выражает благодарность за финансовую поддержку гранта UNAM-PAPIIT IN111421, Национальной системы исследований CONACyT и проекта CONACyT № 86372 программы «Ciencia de Frontera 2019» под названием «Citlalcóatl: многомасштабное исследование на новом рубеже образование и ранняя эволюция звезд и планетных систем», Мексика. DS признает поддержку Deutsche Forschungsgemeinschaft через SPP 1833: «Building a Habitable Earth» (SE 1962/6-1). REP поддерживается грантом Discovery от NSERC.
поддерживается Центром совместных исследований 956, подпроект A6, финансируемый Deutsche Forschungsgemeinschaft (DFG), идентификатор проекта 184018867. Р.К. признает финансовую поддержку через исследовательские гранты Emmy Noether и Heisenberg, финансируемые Немецким исследовательским фондом (DFG) в рамках гранта №. КУ 2849/3 и 2849/9. AP выражает благодарность за финансовую поддержку гранта UNAM-PAPIIT IN111421, Национальной системы исследований CONACyT и проекта CONACyT № 86372 программы «Ciencia de Frontera 2019» под названием «Citlalcóatl: многомасштабное исследование на новом рубеже образование и ранняя эволюция звезд и планетных систем», Мексика. DS признает поддержку Deutsche Forschungsgemeinschaft через SPP 1833: «Building a Habitable Earth» (SE 1962/6-1). REP поддерживается грантом Discovery от NSERC.
Приложение A Карты каналов
В этом разделе мы представляем карты каналов наиболее известных молекул в нашем исследовании.
Рис. A.1 A.1Карты каналов излучения HCN v 2 =1, l =1f с уровнями излучения 5, 6, 7 и 8 σ отмечены белыми контурами. Пурпурными контурами отмечены уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . |
| Рис. А.2 Карты каналов излучения HCN v 2 =1, l =1e с уровнями излучения 3, 5, 6, 7 и 8 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . |
| Рис. А.3 Карты каналов излучения SO 2 с уровнями излучения 3, 5, 6 и 7 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . |
| Рис. А.4 Карты каналов эмиссии HCN(4−3) с уровнями эмиссии 3, 5, 10 и 15 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . |
| Рис. A.5 Карты каналов эмиссии HC 3 N с уровнями эмиссии 3, 5, 6 и 7 σ отмечены белыми контурами. Пурпурными контурами отмечены уровни непрерывного излучения 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . |
Каталожные номера
- Ahmadi, A., Beuther, H., Mottram, J.C., et al. 2018, АиА, 618, А46 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Ахмади, А.
 , Койпер, Р., и Беутер, Х. 2019, A&A, 632, A50 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Койпер, Р., и Беутер, Х. 2019, A&A, 632, A50 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Аньес-Лопес Н., Осорио М., Буске Г. и др. 2020, Ап.Дж., 888, 41 [Перекрестная ссылка] [Google ученый]
- Балли, Дж.
 , и Лада, С.Дж., 1983, ApJ, 265, 824. [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый]
, и Лада, С.Дж., 1983, ApJ, 265, 824. [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый] - Белтран, М. Т., и де Вит, В. Дж. 2016, A&ARv, 24, 6 [Google ученый]
- Benz, A.O., Stäuber, P.
 , Bourke, T.L., et al. 2007, АиА, 475, 549 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Bourke, T.L., et al. 2007, АиА, 475, 549 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Beuther, H., Churchwell, EB, McKee, CF, & Tan, JC 2007, в Protostars and Planets V, eds. Б. Рейпурт, Д. Джуитт и К. Кейл (Тусон: University of Arizona Press), 165.
 [Google ученый]
[Google ученый] - Beuther, H., Mottram, J.C., Ahmadi, A., et al. 2018, А&А, 617, А100 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Beuther, H.
 , Gieser, C., Suri, S., et al. 2021, А&А, 649, А113 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Gieser, C., Suri, S., et al. 2021, А&А, 649, А113 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Боско Ф., Беутер Х., Ахмади А. и др. 2019, А&А, 629, А10 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Кэмпбелл, Б.
 1984, ApJ, 287, 334.
[Google ученый]
1984, ApJ, 287, 334.
[Google ученый] - Чесарони, Р., Санчес-Монж, А., Бельтран, М.Т., и др. 2017, А&А, 602, А59 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Чезарони Р.
 , Беутер Х., Ахмади А. и др. 2019, А&А, 627, А68 [EDP наук]
[Google ученый]
, Беутер Х., Ахмади А. и др. 2019, А&А, 627, А68 [EDP наук]
[Google ученый] - Шабрие, Г. 2003, PASP, 115, 763. [Google ученый]
- Csengeri, T., Bontemps, S., Wyrowski, F., et al. 2018, А&А, 617, А89 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Ди Франческо, Дж.
 , Джонстон, Д., Кирк, Х., Маккензи, Т., и Ледуосинска, Э. 2008, ApJS, 175, 277
[Google ученый]
, Джонстон, Д., Кирк, Х., Маккензи, Т., и Ледуосинска, Э. 2008, ApJS, 175, 277
[Google ученый] - Дрин, Б. Т. 2011, Физика межзвездной и межгалактической среды (Принстон: издательство Принстонского университета) [Google ученый]
- Элицур, М., Холленбах, Д. Дж., и Макки, К. Ф., 1989, ApJ, 346, 983. [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Фэн С.
 , Беутер Х., Хеннинг Т. и др. 2015, А&А, 581, А71 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Беутер Х., Хеннинг Т. и др. 2015, А&А, 581, А71 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Гизер К., Семенов Д., Беутер Х. и соавт. 2019, А&А 631, А142 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Гизер К.
 , Беутер Х., Семенов Д. и др. 2021, А&А, 648, А66 [EDP наук]
[Google ученый]
, Беутер Х., Семенов Д. и др. 2021, А&А, 648, А66 [EDP наук]
[Google ученый] - Гинзбург, А., Балли, Дж., Годди, К., Пламбек, Р., и Райт, М. 2018, ApJ, 860, 119 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Гирарт, Дж.
 М., Фернандес-Лопес, М., Ли, З. Ю. и др. 2018, Ап.Дж., 856, L27 [Перекрестная ссылка]
[Google ученый]
М., Фернандес-Лопес, М., Ли, З. Ю. и др. 2018, Ап.Дж., 856, L27 [Перекрестная ссылка]
[Google ученый] - Gutermuth, R.A., Pipher, J.L., Megeath, S.T., et al. 2011, Ап.Дж., 739, 84 [Google ученый]
- Хакар А., Тафалла М., Форбрич Дж. и соавт. 2018, АиА, 610, А77 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Хильдебранд, Р.
 Х. 1983, QJRAS, 24, 267. [ОБЪЯВЛЕНИЕ НАСА]
[Google ученый]
Х. 1983, QJRAS, 24, 267. [ОБЪЯВЛЕНИЕ НАСА]
[Google ученый] - Или, Дж. Д., Цыгановски, С. Дж., Назари, П., и соавт. 2016, МНИРАН, 462, 4386 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Или, Дж.
 Д., Цыгановски, С. Дж., Броган, С. Л., и соавт. 2018, АпЯ, 869, Л24
[Google ученый]
Д., Цыгановски, С. Дж., Броган, С. Л., и соавт. 2018, АпЯ, 869, Л24
[Google ученый] - Инуцука, С.-и., и Мияма, С.М., 1997, ApJ, 480, 681. [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Янкович М.
 Р., Хаворт Т.Дж., Или Дж.Д. и соавт. 2019, МНИРАН, 482, 4673 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый]
Р., Хаворт Т.Дж., Или Дж.Д. и соавт. 2019, МНИРАН, 482, 4673 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый] - Хименес-Серра, И., Чжан, К., Вити, С., Мартин-Пинтадо, Дж., и де Вит, В. Дж. 2012, ApJ, 753, 34 [Google ученый]
- Джонстон, К.
 Г., Шеперд, Д.С., Робитайл, Т.П., и Вуд, К. 2013, A&A, 551, A43 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
Г., Шеперд, Д.С., Робитайл, Т.П., и Вуд, К. 2013, A&A, 551, A43 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Johnston, K.G., Robitaille, T.P., Beuther, H., et al. 2015, АпЖ, 813, Л19 [Google ученый]
- Джонстон, К.
 Г., Хоар, М.Г., Беутер, Х., и соавт. 2020a, АиА, 634, L11 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
Г., Хоар, М.Г., Беутер, Х., и соавт. 2020a, АиА, 634, L11 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Джонстон, К.Г., Хоар, М.Г., Беутер, Х., и соавт. 2020b, ApJ, 896, 35 [Google ученый]
- Kainulainen, J.
 , Stutz, A.M., Stanke, T., et al. 2017, А&А, 600, А141 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Stutz, A.M., Stanke, T., et al. 2017, А&А, 600, А141 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Классен, М., Пудриц, Р. Э., Койпер, Р., Питерс, Т., и Банерджи, Р. 2016, ApJ, 823, 28 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Краттер, К.
 , и Лодато, Г. 2016, ARA&A, 54, 271
[Google ученый]
, и Лодато, Г. 2016, ARA&A, 54, 271
[Google ученый] - Крупа, П. 2002, Наука, 295, 82 [Google ученый]
- Крамхольц, М.Р., Кляйн, Р.И., Макки, С.Ф., Оффнер, С.С.Р., и Каннингем, А.Дж. 2009, Science, 323, 754 [Google ученый]
- Койпер Р. и Хосокава Т.
 2018, A&A, 616, A101 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
2018, A&A, 616, A101 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Койпер, Р., Клар, Х., Беутер, Х., и Хеннинг, Т. 2010, ApJ, 722, 1556. [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Мацумото Т.
 и Ханава Т. 2003, ApJ, 595, 913.
[Google ученый]
и Ханава Т. 2003, ApJ, 595, 913.
[Google ученый] - Мод, Л.Т., Чезарони, Р., Кумар, М.С.Н., и соавт. 2019, А&А, 628, С1 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Мейер, Д.
 М.А., Воробьев, Е.И., Койпер, Р., и Клей, В. 2017, MNRAS, 464, L90
[Google ученый]
М.А., Воробьев, Е.И., Койпер, Р., и Клей, В. 2017, MNRAS, 464, L90
[Google ученый] - Мейер, Д.М.А., Койпер, Р., Клей, В., Джонстон, К.Г., и Воробьев, Э. 2018, MNRAS, 473, 3615 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Москаделли Л.
 , Санна А., Чезарони Р. и др. 2019, А&А, 622, А206 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Санна А., Чезарони Р. и др. 2019, А&А, 622, А206 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Mottram, J.C., Beuther, H., Ahmadi, A., et al. 2020, А&А, 636, А118 [EDP наук] [Google ученый]
- Müller, H.
 S.P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Структура, 742, 215
[Google ученый]
S.P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Структура, 742, 215
[Google ученый] - Ольгин Ф.А., Хоар М.Г., Джонстон К.Г. и соавт. 2020, МНИРАН, 498, 4721 [Google ученый]
- Олива, Г. А., и Койпер, Р. 2020, A&A, 644, A41 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Оссенкопф, В.
 , и Хеннинг, Т. 1994, A&A, 291, 943.
[Google ученый]
, и Хеннинг, Т. 1994, A&A, 291, 943.
[Google ученый] - Падоан, П., и Нордлунд, О. 2002, ApJ, 576, 870 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Палау А., Эсталелла Р.
 , Джирарт Дж. М. и соавт. 2014, Ап.Дж., 785, 42
[Google ученый]
, Джирарт Дж. М. и соавт. 2014, Ап.Дж., 785, 42
[Google ученый] - Палау, А., Баллестерос-Паредес, Дж., Васкес-Семадени, Э., и др. 2015, МНИРАН, 453, 3785 [Google ученый]
- Палау, А., Сапата, Л.А., Роман-Сунига, К.Г., и соавт. 2018, Ап.Дж., 855, 24 [Google ученый]
- Палла, Ф.
 , и Шталер, С. В. 1993, ApJ, 418, 414.
[Google ученый]
, и Шталер, С. В. 1993, ApJ, 418, 414.
[Google ученый] - Патель Н.А., Куриэль С., Шридхаран Т.К. и соавт. 2005, Природа, 437, 109 [Перекрестная ссылка] [Google ученый]
- Pickett, H.M., Poynter, R.L., Cohen, E.A., et al. 1998, J. Квант. Спектр. Рад. Трансф., 60, 883 [Google ученый]
- Роджерс, С.
 Д., и Чарнли, С. Б. 2001, ApJ, 546, 324.
[Google ученый]
Д., и Чарнли, С. Б. 2001, ApJ, 546, 324.
[Google ученый] - Rygl, K.L.J., Brunthaler, A., Sanna, A., et al. 2012, А&А, 539, А79 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Санчес-Монж, А.
 , Чесарони, Р., Бельтран, М.Т., и соавт. 2013, АиА, 552, L10 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый]
, Чесарони, Р., Бельтран, М.Т., и соавт. 2013, АиА, 552, L10 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[EDP наук]
[Google ученый] - Сэндфорд, С.А., и Алламандола, Л.Дж., 1993, ApJ, 417, 815. [Перекрестная ссылка] [Google ученый]
- Санна, А.
 , Рид, М.Дж., Карраско-Гонсалес, К., и др. 2012, ApJ, 745, 191 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый]
, Рид, М.Дж., Карраско-Гонсалес, К., и др. 2012, ApJ, 745, 191 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый] - Шильке, П. 2015, EAS Pub. Сер., 75–76, 227 [Перекрестная ссылка] [EDP наук] [Google ученый]
- Сейфрид, Д.
 , Санчес-Монж, А., Уолч, С., и Банерджи, Р. 2016, MNRAS, 459, 1892. [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый]
, Санчес-Монж, А., Уолч, С., и Банерджи, Р. 2016, MNRAS, 459, 1892. [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый] - Ширли, Ю. Л. 2015, PASP, 127, 299. [Google ученый]
- Tan, JC, Beltrán, M.
 T., Caselli, P., et al. 2014 г., в Protostars and Planets VI, ред. Х. Беутер, Р. С. Клессен, С. П. Даллемонд и Т. Хеннинг (Тусон: University of Arizona Press), 149.[Google ученый]
T., Caselli, P., et al. 2014 г., в Protostars and Planets VI, ред. Х. Беутер, Р. С. Клессен, С. П. Даллемонд и Т. Хеннинг (Тусон: University of Arizona Press), 149.[Google ученый] - Тобин, Дж. Дж., Луни, Л. В., Ли, З.-Ю., и соавт. 2016, Ап.Дж., 818, 73 [Перекрестная ссылка] [Google ученый]
- Тоомре, А. 1964, ApJ, 139, 1217. [Google ученый]
- Тринидад, М.
 А., Куриэль, С., Канто, Дж., и др. 2003 г., Ап.Дж., 589, 386. [Перекрестная ссылка]
[Google ученый]
А., Куриэль, С., Канто, Дж., и др. 2003 г., Ап.Дж., 589, 386. [Перекрестная ссылка]
[Google ученый] - Uscanga, L., Cantó, J., Gómez, J.F., et al. 2010, ApJ, 715, 132 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [Google ученый]
- Вич, Т.
 Дж., Гроппи, К.Е., и Хедден, А. 2013, ApJ, 765, L34 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый]
Дж., Гроппи, К.Е., и Хедден, А. 2013, ApJ, 765, L34 [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый] - Ван, К.С., ван дер Так, Ф.Ф.С., и Хогерхайде, М.Р. 2012, A&A, 543, A22 [ОБЪЯВЛЕНИЕ НАСА] [Перекрестная ссылка] [EDP наук] [Google ученый]
- Вулфайр, М.
 Г., и Кассинелли, Дж. П. 1987, ApJ, 319, 850. [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый]
Г., и Кассинелли, Дж. П. 1987, ApJ, 319, 850. [ОБЪЯВЛЕНИЕ НАСА]
[Перекрестная ссылка]
[Google ученый] - Чжао Б., Томида К., Хеннебель П. и др. 2020, Космические науки. Обр., 216, 43 [Google ученый]
- Зиннекер, Х.
 , и Йорк, Х.В., 2007 г., ARA&A, 45, 481.
[Google ученый]
, и Йорк, Х.В., 2007 г., ARA&A, 45, 481.
[Google ученый]
1
, где G — гравитационная постоянная, M , R и L — масса, радиус и светимость протозвезды.
2
https://www2.mpia-hd.mpg.de/core/Overview.html
3
http://www.iram.fr/IRAMFR/GILDAS
0KeplerFit находится в свободном доступе на GitHub: https://github.com/felixbosco/KeplerFit
Все таблицы
Таблица 1
Свойства линий, обнаруженных в установке коррелятора 843 мкм.
В тексте
Таблица 2
Свойства ядер, идентифицированных в континууме 843 мкм.
В тексте
Все фигурки
| Рис. 1. Карта плотности потока континуума 843 мкм. Левая панель : черные контуры отмечают уровни непрерывного излучения 843 мкм 3, 5, 6 и 7 σ с σ = 6,7 мЯн луч −1 . Белыми пунктирными контурами отмечены отрицательные уровни излучения 3 σ . Оранжевые контуры отмечают уровни излучения континуума 5, 10, 20, 40 и 80 σ на 1,3 мм ( σ = 0,59 мЯн луч −1 ) на обеих панелях. Правая панель : крупный план центральной области 13 000 а.е. Три ядра, A, B и C, обнаруженные с достоверностью ≥5 σ , отмечены соответствующими метками. Размер луча и масштабная линейка наблюдений 843 мкм показаны в нижнем левом и верхнем левом углу каждой панели соответственно. Красная звезда на обеих панелях указывает положение протозвезды, предполагая, что она расположена на пике континуума 1,3 мм. | |
| В тексте | |
Рис. 2 2Верхняя панель: спектр низкого спектрального разрешения , пространственно усредненный по области 0″,7 × 0″,7 с центром в точке δ = +40°11′19′′.216, охватывающий ядра A, B, C. Средняя панель : увеличение диапазона частот от 354,2 до 355,3 ГГц. Нижняя панель : увеличение диапазона частот от 356,4 до 357,1 ГГц. Горизонтальная серая пунктирная линия соответствует 5 σ уровень отношения сигнал/шум ( σ = 3,4 мЯн луч −1 ). | |
| В тексте | |
| Рис. 3 Спектры пяти наиболее заметных переходов к центру жил A (, верхняя панель, ), B (, средняя панель, ) и C (, нижняя панель, ), усредненные по размеру луча. Вертикальная серая пунктирная линия указывает скорость источника. | |
| В тексте | |
| Рис. 4 Карты моментов пяти наиболее заметных линий в наших наблюдениях. | |
| В тексте | |
| Рис. 5 Левая панель : взвешенная по интенсивности карта пиковой скорости усредненного колебательно-возбужденного излучения HCN. Черными контурами отмечена эмиссия континуума 3, 5, 6 и 7 σ 843 мкм. Стрелки показывают направление крупномасштабного оттока с востока на запад, наблюдаемого в выбросе CO(2−1), синим и красным цветами показаны линейные выбросы с синим и красным смещением (см. Gieser et al. 2019).). Правая панель : PV-диаграмма для усредненной колебательно-возбужденной эмиссии HCN, извлеченная из среза вдоль пунктирной линии, показанной на левой панели. | |
| В тексте | |
| Рис. 6 Карта Toomre Q взята из Ahmadi et al. (в подготовке) с наложенными белыми контурами континуума 843 мкм (3, 5, 6 и 7 σ ) и местоположениями водного мазера из Санны и др. (2012). Водяные мазеры показаны цветными крестами, где цвет представляет их лучевую скорость, а для их местоположения мы используем то же соглашение об именах северо-восток (СВ), юго-восток (ЮВ) и средний запад (СВ), что и Санна и др. | |
| В тексте | |
| Рис. A.1 Карты каналов излучения HCN v 2 =1, l =1f с уровнями излучения 5, 6, 7 и 8 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . | |
| В тексте | |
| Рис. А.2 Карты каналов излучения HCN v 2 =1, l =1e с уровнями излучения 3, 5, 6, 7 и 8 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . | |
| В тексте | |
Рис. А.3 А.3Карты каналов излучения SO 2 с уровнями излучения 3, 5, 6 и 7 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . | |
| В тексте | |
| Рис. А.4 Карты каналов эмиссии HCN(4−3) с уровнями эмиссии 3, 5, 10 и 15 σ отмечены белыми контурами. Пурпурные контуры обозначают уровни излучения континуума 843 мкм 3, 5, 6 и 7 σ . Синие пунктирные контуры обозначают эмиссию в линии − 3 σ . | |
| В тексте | |
| Рис. A.5 Карты каналов эмиссии HC 3 N с уровнями эмиссии 3, 5, 6 и 7 σ отмечены белыми контурами. Пурпурными контурами отмечены уровни непрерывного излучения 843 мкм 3, 5, 6 и 7 σ . | |
| В тексте | |
Моделирование глубоких щелей, создаваемых планетами-гигантами в протопланетных дисках | Публикации Астрономического общества Японии
Журнальная статья
Казухиро Д. Канагава,
Казухиро Д. Канагава
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Хидэкадзу Танака,
Хидэкадзу Танака
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Такаюки Муто,
Такаюки Муто
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Такаюки Танигава
Такаюки Танигава
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Публикации Астрономического общества Японии , том 69, выпуск 6, декабрь 2017 г. , 97, https://doi.org/10.1093/pasj/psx114
, 97, https://doi.org/10.1093/pasj/psx114
Опубликовано:
15 ноября 2017 г.
033
История статьиПолучено:
19 июня 2017 г.
Принято:
14 сентября 2017 г.
Опубликовано:
15 ноября 2017 г.
Фильтр поиска панели навигации Публикации Астрономического общества ЯпонииНастоящий выпускаккреция, аккреционные дискивзаимодействия планет-дисковпланеты и спутники: формирование протопланетных дисковАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Публикации Астрономического общества ЯпонииНастоящий выпускаккреция, аккреционные дискивзаимодействия планет с дискамипланеты и спутники: формирование протопланетных дисковАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Гигантская планета, встроенная в протопланетный диск, образует брешь. Этот процесс важен как для теории, так и для наблюдений. Используя результаты исследования для широкого диапазона параметров при двумерном гидродинамическом моделировании, мы построили эмпирическую формулу для структуры зазора (т. е. радиального распределения поверхностной плотности), которая может воспроизводить ширину и глубину зазора, полученные при двумерном моделировании. . Эта формула позволяет нам судить о том, вызван ли наблюдаемый зазор вкрапленной планетой или нет. Распространение волн, запускаемых планетой, тесно связано со структурой щели. Это делает зазор шире и меньше по сравнению со случаем, когда предполагается мгновенное затухание волны. Гидродинамическое моделирование показывает, что волны не затухают сразу в точке запуска волн, даже если планета такая же массивная, как Юпитер. По результатам гидродинамического моделирования также получена эмпирическая модель распространения и затухания волн в случаях глубоких зазоров. Одномерная модель зазора с нашей моделью распространения волн способна хорошо воспроизводить структуры зазора в гидродинамическом моделировании.
Этот процесс важен как для теории, так и для наблюдений. Используя результаты исследования для широкого диапазона параметров при двумерном гидродинамическом моделировании, мы построили эмпирическую формулу для структуры зазора (т. е. радиального распределения поверхностной плотности), которая может воспроизводить ширину и глубину зазора, полученные при двумерном моделировании. . Эта формула позволяет нам судить о том, вызван ли наблюдаемый зазор вкрапленной планетой или нет. Распространение волн, запускаемых планетой, тесно связано со структурой щели. Это делает зазор шире и меньше по сравнению со случаем, когда предполагается мгновенное затухание волны. Гидродинамическое моделирование показывает, что волны не затухают сразу в точке запуска волн, даже если планета такая же массивная, как Юпитер. По результатам гидродинамического моделирования также получена эмпирическая модель распространения и затухания волн в случаях глубоких зазоров. Одномерная модель зазора с нашей моделью распространения волн способна хорошо воспроизводить структуры зазора в гидродинамическом моделировании. В случае планеты с массой Юпитера мы также обнаружили, что волны с меньшим волновым числом (например, м = 2) возбуждаются и переносят угловой момент в место, далекое от планеты. Волна с м = 2 тесно связана с вторичной волной, запущенной противоположным от планеты участком.
В случае планеты с массой Юпитера мы также обнаружили, что волны с меньшим волновым числом (например, м = 2) возбуждаются и переносят угловой момент в место, далекое от планеты. Волна с м = 2 тесно связана с вторичной волной, запущенной противоположным от планеты участком.
1 Введение
За последнее десятилетие было открыто более тысячи внесолнечных планет. Исследование внесолнечных планет выявило разнообразие планет-гигантов за пределами Солнечной системы (например, Burke et al. 2014). Планеты-гиганты рождаются в протопланетных дисках в результате аккреции ядра (например, Mizuno 1980; Kanagawa & Fujimoto 2013) или гравитационной нестабильности газового диска (например, Cameron 1978; Zhu et al. 2012a). После образования они претерпевают орбитальную миграцию, а газовая аккреция приводит к росту их массы. С такими процессами тесно связано разнообразие внесолнечных планет (например, Мордасини и др. , 2012; Ида и др., 2013).
, 2012; Ида и др., 2013).
Области формирования планет в протопланетных дисках теперь могут быть отображены напрямую, например, с помощью Большой миллиметровой/субмиллиметровой матрицы Атакамы (ALMA) и оптических и/или ближних инфракрасных телескопов восьмиметрового класса. Изображения с высоким разрешением выявили наличие сложных морфологических структур в дисках: эти структуры включают спирали (например, Муто и др., 2012 г.; Грейди и др., 2013 г.; Кристианс и др., 2014 г.; Бенисти и др., 2015 г.; Карри и др., 2015 г.). 2015; Акияма и др., 2016) и пробелы (например, Осорио и др., 2014; ALMA Partnership и др., 2015; Момосе и др., 2015; Акияма и др., 2015; Номура и др., 2016; Йен и др., 2016; Цукагоши и др., 2016 г.). Прямые изображения в настоящее время находят возможные признаки формирования планет в дисках (например, Саллум и др., 2015 г.). Чтобы понять происхождение дисковых структур и их возможную связь с образованием планет, важно построить соответствующую количественную модель.
Планета гравитационно взаимодействует с газом в окружающем диске, в результате чего планета возбуждает волны плотности (спирали). Если планета достаточно массивна, она также создает щелевые структуры (например, Lin & Papaloizou 1979; Goldreich & Tremaine 1980; Artymowicz & Lubow 1994; Kley 1999; Crida et al. 2006). Недавно был проведен ряд исследований количественной зависимости между массой планеты и структурой щели (т. е. глубиной и шириной) (Duffell & MacFadyen, 2013; Fung et al., 2014; Kanagawa et al., 2015a, 2016; Duffell & Chiang 2015; Fung & Chiang 2016), и обсуждалось их применение к реальным наблюдениям (Kanagawa et al. 2015a; Momose et al. 2015; van der Marel et al. 2016; Nomura et al. 2016; Tsukagoshi et al. 2016). Тем не менее, есть еще возможности для улучшения текущих моделей. Канагава и соавт. (2016) представили эмпирическую формулу для ширины зазора: они определили ее как место, в котором поверхностная плотность зазора уменьшается до 50% от исходного значения. Общая структура разрыва, созданного планетой, требует дальнейшего изучения.
Структура щели тесно связана с затуханием спиральных волн плотности, возбуждаемых планетой, поскольку планета передает угловой момент диску через волны (например, Такеучи и др., 1996; Гудман, Рафиков, 2001; Рафиков, 2002; Донг и др., 2011 г.). Даффелл (2015) построил аналитические модели структуры щели, используя модель затухания волн Гудмана и Рафикова (2001), которая особенно полезна в случае неглубоких щелей (создаваемых относительно маломассивными планетами). Однако распространение волн в случае, когда глубокая щель образована планетой с большой массой, еще недостаточно изучена. Распространение волн, вызванных планетой с большой массой, будет качественно отличаться от распространения в случае планеты с малой массой, как следует из параметризованного исследования Канагава и др. (2015b, далее К15).
В этой статье мы расширяем нашу предыдущую модель ширины и глубины зазора и представляем полную модель формы зазора; это основано на ряде двумерных долгосрочных гидродинамических симуляций. Мы также предоставляем модель распространения волны, показанную гидродинамическим моделированием, когда формируется глубокая щель. В разделе 2 мы кратко суммируем настройку выполненного нами численного моделирования. В разделе 3 мы получаем эмпирическую формулу для структуры зазора, показывающую результаты гидродинамического моделирования. Из этой эмпирической формулы структуры щели можно построить эмпирическую модель распространения волн плотности. В разделе 4 мы получаем эмпирическую модель распространения волны. Приняв эту модель распространения волны, мы обеспечиваем полуаналитическую радиальную одномерную модель структуры зазора, которая способна воспроизвести структуры зазора, заданные двумерным моделированием. В разделе 5 мы обсуждаем наблюдательное применение нашей формулы. Мы также обсуждаем, как возбуждение и распространение волн меняются вместе с увеличением массы планеты, показывая результаты двумерного гидродинамического моделирования. В этот раздел включено обсуждение гидродинамических неустойчивостей, таких как неустойчивость Рэлея и неустойчивость волн Россби.
Мы также предоставляем модель распространения волны, показанную гидродинамическим моделированием, когда формируется глубокая щель. В разделе 2 мы кратко суммируем настройку выполненного нами численного моделирования. В разделе 3 мы получаем эмпирическую формулу для структуры зазора, показывающую результаты гидродинамического моделирования. Из этой эмпирической формулы структуры щели можно построить эмпирическую модель распространения волн плотности. В разделе 4 мы получаем эмпирическую модель распространения волны. Приняв эту модель распространения волны, мы обеспечиваем полуаналитическую радиальную одномерную модель структуры зазора, которая способна воспроизвести структуры зазора, заданные двумерным моделированием. В разделе 5 мы обсуждаем наблюдательное применение нашей формулы. Мы также обсуждаем, как возбуждение и распространение волн меняются вместе с увеличением массы планеты, показывая результаты двумерного гидродинамического моделирования. В этот раздел включено обсуждение гидродинамических неустойчивостей, таких как неустойчивость Рэлея и неустойчивость волн Россби. Раздел 6 содержит резюме и обсуждение.
Раздел 6 содержит резюме и обсуждение.
2 Краткий обзор настройки численного моделирования
Kanagawa et al. (2016) выполнили ряд двумерных симуляций в широком диапазоне параметров (масса планеты, высота диска и вязкость) и получили зависимость между шириной зазора и массой планеты. В этой статье мы расширяем модель путем дальнейшего анализа численного моделирования. В этом разделе мы кратко рассмотрим настройку гидродинамического моделирования.
Численно рассчитаны процессы образования щели в протопланетном диске при наличии планеты. Мы предполагали геометрически тонкий и несамогравитирующий диск. Мы приняли двумерную цилиндрическую систему координат ( R , ϕ), а начало координат располагалось в положении центральной звезды. Мы приняли простое локально изотермическое уравнение состояния, и распределение температуры не зависит от времени. Масса центральной звезды также постоянна во время моделирования. С помощью алгоритма FARGO (Masset, 2000), который широко используется при изучении взаимодействия диска с планетой (например, Crida & Morbidelli, 2007; Baruteau et al., 2011; Zhu et al., 2011), мы решили уравнения неразрывности и движения дисковый газ. В этой статье мы принимаем α-рецепт Шакуры и Сюняева 19.73, и тогда кинетическая вязкость записывается как ν = α ч 2 Ω k −1 , где ч и Ω k — высота диска по шкале и кеплеровская угловая скорость соответственно.
С помощью алгоритма FARGO (Masset, 2000), который широко используется при изучении взаимодействия диска с планетой (например, Crida & Morbidelli, 2007; Baruteau et al., 2011; Zhu et al., 2011), мы решили уравнения неразрывности и движения дисковый газ. В этой статье мы принимаем α-рецепт Шакуры и Сюняева 19.73, и тогда кинетическая вязкость записывается как ν = α ч 2 Ω k −1 , где ч и Ω k — высота диска по шкале и кеплеровская угловая скорость соответственно.
Исходные структуры диска, граничные условия и другие вычислительные установки (например, вычислительная область и разрешения) такие же, как в Kanagawa et al. (2016). Чтобы завершить обзор параметров, мы дополнительно провели шесть симуляций с h p / R p = 2/15, где h p — высота диска в точке r p , которая является радиусом орбиты планеты; ( M p / M * , α) = (10 −3 , 4×10 −3 ), (2×10×−3 , 0 ), (5 × 10 −4 , 10 −3 ), (10 −3 , 10 −3 ), (5 × 10 −4 , 6,4 × 10 −4 ) и (10 -3 , 6,4 × 10 -4 ) (всего 32 прогона). We also ran 2 simulations with small planet mass of m pl / m ☆ = 5 × 10 −5 , where m pl and m ☆ are the masses of планета и центральная звезда соответственно; (α, h p / r p ) = (10 −3 , 1/20) и (10 −3 , 1/25). Обзор охватывает диапазон массы планеты в единицах массы центральной звезды как 5 × 10 −5 < M p / M * < 2 × 10 −3 , the range of the disk aspect ratio as 1/30 < h p / R p < 2/15, а диапазон вязкости диска α как 10 −4 < α < 10 −2 . Набор параметров каждого прогона описан в Kanagawa et al. (2016), за исключением дополнительных тиражей, упомянутых выше.
We also ran 2 simulations with small planet mass of m pl / m ☆ = 5 × 10 −5 , where m pl and m ☆ are the masses of планета и центральная звезда соответственно; (α, h p / r p ) = (10 −3 , 1/20) и (10 −3 , 1/25). Обзор охватывает диапазон массы планеты в единицах массы центральной звезды как 5 × 10 −5 < M p / M * < 2 × 10 −3 , the range of the disk aspect ratio as 1/30 < h p / R p < 2/15, а диапазон вязкости диска α как 10 −4 < α < 10 −2 . Набор параметров каждого прогона описан в Kanagawa et al. (2016), за исключением дополнительных тиражей, упомянутых выше.
Щель открывается взаимодействием диска с планетой и закрывается вязкой диффузией. В установившемся режиме поток вязкого углового момента уравновешивается планетарным крутящим моментом. Шкала времени открытия разрыва будет масштабироваться по шкале вязкого времени (например, Lynden-Bell & Pringle 192/\nu$|) или время жизни диска (∼1 млн лет). Следовательно, можно наблюдать разрыв на всю ширину.
В установившемся режиме поток вязкого углового момента уравновешивается планетарным крутящим моментом. Шкала времени открытия разрыва будет масштабироваться по шкале вязкого времени (например, Lynden-Bell & Pringle 192/\nu$|) или время жизни диска (∼1 млн лет). Следовательно, можно наблюдать разрыв на всю ширину.
3 Эмпирическая формула для структуры разрыва
В этом разделе мы получаем эмпирическую формулу для радиальной структуры разрыва, вызванного планетой, в стационарном состоянии. Канагава и соавт. (2016) нашли масштабное соотношение ширины щели, которая определяется радиальной шириной области, где поверхностная плотность меньше порога плотности Σ th = 0,5 Σ 0 . Во-первых, здесь мы показываем, что это скейлинговое соотношение может быть расширено, даже когда порог плотности отличен от 0,5Σ 0 . Как показано на левой панели рисунка 1, мы измеряем ширину зазора для Σ th = 0,1Σ 0 , 0,3Σ 0 , 0,5Σ 0 и 0,8Σ 0 . На правой панели рисунка 1 показана ширина зазора с каждым Σ th в пересчете на K ΄. Как видно из рисунка, ширина зазора, определяемая Σ th = 0,1Σ 0 и 0,3Σ 0 , пропорциональна K ΄ 1/4 , как видно с Σ -й = 0,5Σ 0 . Обратите внимание, что мы подтвердили, что ширины, показанные на рисунке, достигают устойчивых значений при t ≃ t по отношению к , заданных уравнением (3) (см. приложение 1). Хотя ширина зазора, определяемая Σ th = 0,8 Σ 0 , немного отклоняется от линии, определяемой ∝ K ΄ 1/4 для K ΄ ≲ 52 K K K ΄ ≲ 1, 1/4 . Мы получаем масштабное соотношение, в том числе показанное Kanagawa et al. (2016) как 9{\ простое число 1/4}.
\end{eqnarray}
На правой панели рисунка 1 показана ширина зазора с каждым Σ th в пересчете на K ΄. Как видно из рисунка, ширина зазора, определяемая Σ th = 0,1Σ 0 и 0,3Σ 0 , пропорциональна K ΄ 1/4 , как видно с Σ -й = 0,5Σ 0 . Обратите внимание, что мы подтвердили, что ширины, показанные на рисунке, достигают устойчивых значений при t ≃ t по отношению к , заданных уравнением (3) (см. приложение 1). Хотя ширина зазора, определяемая Σ th = 0,8 Σ 0 , немного отклоняется от линии, определяемой ∝ K ΄ 1/4 для K ΄ ≲ 52 K K K ΄ ≲ 1, 1/4 . Мы получаем масштабное соотношение, в том числе показанное Kanagawa et al. (2016) как 9{\ простое число 1/4}.
\end{eqnarray}
(5)
Это скейлинговое соотношение согласуется с результатами предыдущих гидродинамических расчетов (см. приложение 2). Обратите внимание, что приведенное выше соотношение соответствует уравнению (1), когда Σ th / Σ 0 = 0,5. Уравнение (5) хорошо согласуется с ширинами зазоров, показанными на рисунке 1.
приложение 2). Обратите внимание, что приведенное выше соотношение соответствует уравнению (1), когда Σ th / Σ 0 = 0,5. Уравнение (5) хорошо согласуется с ширинами зазоров, показанными на рисунке 1.
Рис. 1.
Открыть в новой вкладкеСкачать слайд
(Слева) Схематическое изображение измерения ширины зазоров с различными Σ -й . (Справа) Ширина зазора с Σ th = 0,1Σ 0 , 0,3Σ 0 , 0,5Σ 0 и 0,8Σ 0 . Тонкими линиями показаны результаты для уравнения (5) с Σ th = 0,1Σ 0 , 0,3Σ 0 , 0,5Σ 0 и 0,8Σ 0 (снизу). (В цвете онлайн)
Формулу радиального распределения плотности газа можно вывести из уравнения (5), установив Σ th = Σ( R ) и Δ зазора = 2| R − R p | как
\begin{eqnarray}
\Sigma (R) = \left\lbrace \begin{array}{ll}\Sigma _{\min } &\ \mbox{for}\ \ |RR _{\rm p}|<\Delta R_1,\ \
\Sigma _{\rm gap}(R) &\ \mbox{for}\ \\Delta R_1< |RR _{\rm p}| < \Дельта R_2,\\
\Sigma _0 &\ \mbox{for}\ \ |R-R_{\rm p}|> \Delta R_2, \end{массив}\right. {\prime -1/4} \frac{|RR _{\rm p}|}{R_{\ рм р}} — 0,32,
\end{эквнаррай} 9{-1}.
\end{eqnarray}
{\prime -1/4} \frac{|RR _{\rm p}|}{R_{\ рм р}} — 0,32,
\end{эквнаррай} 9{-1}.
\end{eqnarray}
(11)
Мы иллюстрируем поверхностную плотность, заданную эмпирической формулой уравнения (6), вместе с результатами гидродинамического моделирования на рисунке 2. В верхнем ряду рисунка мы показываем разрыв Структуры M P / M * = 5 × 10 −4 до 10 -3 для H P /3323 H P /33323 H P /33323 H P /33 2324 . 10 −3 . В этом случае уравнение (6) точно воспроизводит структуры зазоров, полученные при двумерном гидродинамическом моделировании. Во второй и третьей строках показаны структуры гэпов M p / M * = 10 −3 и 5 × 10 −4 соответственно для различных соотношений сторон диска и вязкости. Как показано в верхней строке, уравнение (6) точно воспроизводит результаты гидродинамического моделирования. В нижнем ряду показаны структуры пробелов M p / M * = 10 −4 . Для (α, h p / R p ) = (10 −4 , 1/20) и (10 −3 , 1/25), мы все еще можем подогнать уравнение (6) к структуре зазора моделирования, но для (α, h p / R p ) = (10 −3 , 1/20), зазор, полученный в результате моделирования, шире, чем указанный в уравнении. Уравнение (6) не дает хорошей оценки, когда зазор неглубокий; то есть Σ мин ≳ 0,5Σ 0 .
Как показано в верхней строке, уравнение (6) точно воспроизводит результаты гидродинамического моделирования. В нижнем ряду показаны структуры пробелов M p / M * = 10 −4 . Для (α, h p / R p ) = (10 −4 , 1/20) и (10 −3 , 1/25), мы все еще можем подогнать уравнение (6) к структуре зазора моделирования, но для (α, h p / R p ) = (10 −3 , 1/20), зазор, полученный в результате моделирования, шире, чем указанный в уравнении. Уравнение (6) не дает хорошей оценки, когда зазор неглубокий; то есть Σ мин ≳ 0,5Σ 0 .
Рис. 2.
Открыть в новой вкладкеСкачать слайд
Азимутальные усредненные поверхностные плотности, заданные эмпирической формулой уравнения (6) (сплошная линия) и результатами гидродинамического моделирования (штриховая линия) для различных наборов массы планеты, аспекта диска отношение и вязкость. (В цвете онлайн)
(В цвете онлайн)
Crida, Morbidelli, and Masset (2006) представили полуаналитическую модель глубоких разрывов. Они ввели «крутящий момент давления» и рассмотрели баланс между крутящим моментом давления, планетарным крутящим моментом и потоком вязкого углового момента. На рисунке 3 мы сравниваем радиальные структуры зазоров, заданные уравнением (6) и Крида, Морбиделли и Массет (2006). Мы получаем модель Криды на рисунке, решая уравнение (14) Криды, Морбиделли и Массета (2006). При расчете модели Криды мы принимаем Σ 0 значение, которое в 1,5 раза больше нашего, чтобы установить Σ вне разрыва в модели Криды на тот же уровень, что и в нашей модели. Модели Crida дают значительно более мелкие зазоры по сравнению с зазорами, полученными в двумерном моделировании с нашим набором параметров. Уравнение (6) хорошо воспроизводит глубину зазора в случае параметров, представленных на правой нижней панели рисунка 3. В случае α = 10 −3 , h p / R стр. = 1/20 и M p / M * = 10 −3 (правая нижняя панель), глубина зазора, полученная по уравнению (6), примерно в пять раз меньше, чем что в симуляции. Это несоответствие частично происходит из-за того, что газ не вращается с кеплеровской скоростью. Мы предоставляем полуаналитическую модель, учитывающую этот эффект, в разделе 4. Для ширины зазора как уравнение (6), так и модель Крайда разумно согласуются с двумерным моделированием. Однако, когда масса планеты мала, модель Крайда дает более узкие промежутки, чем моделирование, как видно из левой нижней панели на рисунке 3.
= 1/20 и M p / M * = 10 −3 (правая нижняя панель), глубина зазора, полученная по уравнению (6), примерно в пять раз меньше, чем что в симуляции. Это несоответствие частично происходит из-за того, что газ не вращается с кеплеровской скоростью. Мы предоставляем полуаналитическую модель, учитывающую этот эффект, в разделе 4. Для ширины зазора как уравнение (6), так и модель Крайда разумно согласуются с двумерным моделированием. Однако, когда масса планеты мала, модель Крайда дает более узкие промежутки, чем моделирование, как видно из левой нижней панели на рисунке 3.
Рис. 3.
Открыть в новой вкладкеСкачать слайд
Сравнение уравнения (6) (сплошная линия) и модели Crida, Morbidelli, and Masset (2006) (пунктирная линия). Толстые пунктирные линии — результаты двумерного гидродинамического моделирования. (В цвете онлайн)
4 Полуаналитические модели структур радиального зазора
4.
 1 Модель распространения волн
1 Модель распространения волнПланета обменивается угловым моментом с окружающим газом диска посредством волн плотности. Как указывалось в предыдущих исследованиях (например, Петрович и Рафиков 2012; К15), распространение волн плотности напрямую связано с распределением поверхностной плотности зазора. Планета передает свой угловой момент волнам плотности. Затем угловой момент от планеты переносится волнами. Наконец, угловой момент передается газу диска за счет рассеяния волн (например, Такеучи и др. 19).{\rm волна}(R)$|, которая определяется уравнением (A5). На рисунке 4 мы показываем схематическое изображение эффекта распространения волны. (подробности см. в K15 и приложении 3).
Рис. 4.
Открыть в новой вкладкеСкачать слайд
Схематическое изображение передачи углового момента за счет волн плотности. Распространение волны вызывает разницу между суммарным планетарным крутящим моментом T p и накопленным крутящим моментом T d . 2$| в области разрыва (К15). Тогда мы перепишем уравнение (12) в виде 92 \ Omega _ {k, p} F _ {\ rm M} + T _ {\ rm d} (R).}
\end{eqnarray}
2$| в области разрыва (К15). Тогда мы перепишем уравнение (12) в виде 92 \ Omega _ {k, p} F _ {\ rm M} + T _ {\ rm d} (R).}
\end{eqnarray}
(13)
Как показано в уравнении (13), распределение поверхностной плотности определяется, если задана функция T d . Функция T d неявно зависит от поверхностной плотности, потому что T d зависит от крутящего момента, создаваемого планетой, который определяется распределением поверхностной плотности. Чтобы получить распределения поверхностной плотности и крутящего момента, требуется итерационный метод (см. K15).
Распространение волн, запускаемых планетой, изучалось, например, Гудманом и Рафиковым (2001). Их модель указывает на то, что волны, запущенные достаточно массивной планетой [ M P > M 1 = (2/3) ( H P / R 4. 3. 3. 3. . 3. 4. 3. 3. 3. . 3. . 3. M * ≃ 1 × 10 −4 M * ] затухает из-за слабого скачка, развивающегося вблизи точки запуска волны плотности. Из-за удара угловой момент волн уменьшается как | R − R p | 5/4 из места удара. Используя модель распространения волн Гудмана и Рафикова (2001), Даффелл (2015) предложил аналитическую модель структуры зазора. Его модель способна точно воспроизвести структуру щели, если щель неглубокая. Однако, когда зазор велик, модель Даффелла (2015) предсказывает гораздо более узкий зазор, чем полученный с помощью численного моделирования, что означает, что вклад углового момента от волн менее эффективен, чем тот, который предсказывает модель Гудмана и Рафикова. (2001). Для глубокой щели К15 представил простую модель распространения волны с использованием двух свободных параметров 9{\ infty} $ | представляет собой общий крутящий момент возбуждения, создаваемый планетой (подробности см.
3. 3. . 3. 4. 3. 3. 3. . 3. . 3. M * ≃ 1 × 10 −4 M * ] затухает из-за слабого скачка, развивающегося вблизи точки запуска волны плотности. Из-за удара угловой момент волн уменьшается как | R − R p | 5/4 из места удара. Используя модель распространения волн Гудмана и Рафикова (2001), Даффелл (2015) предложил аналитическую модель структуры зазора. Его модель способна точно воспроизвести структуру щели, если щель неглубокая. Однако, когда зазор велик, модель Даффелла (2015) предсказывает гораздо более узкий зазор, чем полученный с помощью численного моделирования, что означает, что вклад углового момента от волн менее эффективен, чем тот, который предсказывает модель Гудмана и Рафикова. (2001). Для глубокой щели К15 представил простую модель распространения волны с использованием двух свободных параметров 9{\ infty} $ | представляет собой общий крутящий момент возбуждения, создаваемый планетой (подробности см. в приложении 3). Если предположить, что форма крутящего момента определяется уравнением (14), мы можем получить форму зазора, используя уравнение (12). Следует, однако, отметить, что уравнение (14) является чисто параметризованной моделью для T d ( R ), и его правильность должна быть проверена с помощью численного моделирования. В частности, распределение поверхностной плотности зазора сильно зависит от выбора двух свободных параметров x d и w d и, следовательно, реалистичные значения этих параметров должны быть определены с помощью численного моделирования.
в приложении 3). Если предположить, что форма крутящего момента определяется уравнением (14), мы можем получить форму зазора, используя уравнение (12). Следует, однако, отметить, что уравнение (14) является чисто параметризованной моделью для T d ( R ), и его правильность должна быть проверена с помощью численного моделирования. В частности, распределение поверхностной плотности зазора сильно зависит от выбора двух свободных параметров x d и w d и, следовательно, реалистичные значения этих параметров должны быть определены с помощью численного моделирования.
Руководствуясь уравнением (6) распределения поверхностной плотности, эмпирически определяем параметры x d и w d как
\begin{eqnarray} x_{\rm d}& =& R_{\rm p}\, \pm \, \frac{\Delta R_2+\Delta R_1}{2} , \end{eqnarray}
(15)
\begin{eqnarray} w_{\rm d}& =& \Delta R_2-\Delta R_1 , \end{eqnarray}
(16)
где Δ R 1 и Δ R 2 определяются уравнениями (8) и (9) соответственно, а знак х d является положительным, когда R > R p , и отрицательным, когда R < R p . На рисунке 5 показаны совокупные крутящие моменты, приложенные к диску, заданные уравнением (12) и двумерным гидродинамическим моделированием. Кумулятивный крутящий момент, определяемый уравнением (14) с уравнениями (15) и (16), разумно воспроизводит результаты двумерного гидродинамического моделирования.
На рисунке 5 показаны совокупные крутящие моменты, приложенные к диску, заданные уравнением (12) и двумерным гидродинамическим моделированием. Кумулятивный крутящий момент, определяемый уравнением (14) с уравнениями (15) и (16), разумно воспроизводит результаты двумерного гидродинамического моделирования.
Рис. 5.
Открыть в новой вкладкеСкачать слайд
Совокупный крутящий момент на диске, полученный по уравнению (14) (сплошные линии) и гидродинамическому моделированию (пунктирные линии). (В цвете онлайн)
Мы используем формулу ВКБ (например, Ward 1986) для расчета момента возбуждения. Однако мы должны учитывать нелинейные эффекты, так как в этой статье мы имеем дело с относительно массивными планетами, создающими глубокие промежутки. Согласно Миёси и соавт. (1999), нелинейный эффект снижает момент возбуждения по сравнению с ожидаемым согласно линейной теории. Чтобы учесть нелинейный эффект, введем понижающий коэффициент f NL (<1) и умножьте этот коэффициент на плотность крутящего момента (подробности см. в приложении 3). Как показано ниже, f NL = 0,4 лучше воспроизводит глубину зазора, полученную с помощью численного гидродинамического моделирования. Поскольку мы рассматриваем случаи, когда M p > ( h p / R p ) 3 , коэффициент f 3 L 902 всегда равен 24 L 902.
в приложении 3). Как показано ниже, f NL = 0,4 лучше воспроизводит глубину зазора, полученную с помощью численного гидродинамического моделирования. Поскольку мы рассматриваем случаи, когда M p > ( h p / R p ) 3 , коэффициент f 3 L 902 всегда равен 24 L 902.
4.2 Конструкции с радиальным зазором
На рисунке 6 показана радиальная структура зазора, рассчитанная путем решения уравнения (13) с x d и w d , заданными уравнениями (15) и (16). Для сравнения на рисунке изображены структуры зазоров, полученные с помощью двумерного гидродинамического моделирования и уравнения (6). Решения уравнения (12) хорошо согласуются по ширине и глубине с гидродинамическим моделированием для различных высот диска и вязкости, пока масса планеты относительно велика. Поскольку в полуаналитической модели учитывается отклонение от кеплеровского вращения, структура дна щели более гладкая, а щель несколько глубже, чем те, что задаются уравнением (6). Когда α = 10 −3 и h p / R p = 1/25 (правая нижняя часть рисунка 6), полуаналитическая модель [уравнение (12)] дает зазор, который приблизительно в три раза меньше, чем дает двумерное моделирование. Мы считаем, что полуаналитическая модель обеспечивает разумное соответствие глубоким промежуткам, созданным планетой.
Поскольку в полуаналитической модели учитывается отклонение от кеплеровского вращения, структура дна щели более гладкая, а щель несколько глубже, чем те, что задаются уравнением (6). Когда α = 10 −3 и h p / R p = 1/25 (правая нижняя часть рисунка 6), полуаналитическая модель [уравнение (12)] дает зазор, который приблизительно в три раза меньше, чем дает двумерное моделирование. Мы считаем, что полуаналитическая модель обеспечивает разумное соответствие глубоким промежуткам, созданным планетой.
Рис. 6.
Открыть в новой вкладкеСкачать слайд
Поверхностные плотности, полученные по уравнению (12) (сплошные линии) и гидродинамическому моделированию (толстые пунктирные линии). Для сравнения также наносим поверхностную плотность, определяемую уравнением (6) (пунктирные линии). (В цвете онлайн)
На левой панели рисунка 7 показана минимальная поверхностная плотность зазора Σ мин , полученная по одномерной модели с f NL = 0,4 и 1,0. Мы также наносим на график минимальное значение усредненной по азимуту поверхностной плотности, полученное при двумерном моделировании. Когда зазор невелик, как K < 10 2 , одномерная модель [уравнение (13)] дает нам значение Σ мин , аналогичное полученному при двумерном моделировании, которое также согласуется с уравнением (10), в случаях обоих f NL = 0,4 и 1 (но более подходящей выглядит модель с f NL = 1). Так как разрыв в K > 10 2 глубже, то одномерная модель с f NL = 1 дает нам гораздо меньшее Σ мин по сравнению с уравнением (10) (а двумерная симуляции). С другой стороны, Σ мин , полученные с помощью одномерной модели, согласуются с данными, полученными с помощью двумерного моделирования и уравнения (10). Для очень глубоких зазоров с K > 10 3 , Σ мин , заданное двумерным моделированием, меньше, чем предсказывает эмпирическая формула уравнения (10).
Мы также наносим на график минимальное значение усредненной по азимуту поверхностной плотности, полученное при двумерном моделировании. Когда зазор невелик, как K < 10 2 , одномерная модель [уравнение (13)] дает нам значение Σ мин , аналогичное полученному при двумерном моделировании, которое также согласуется с уравнением (10), в случаях обоих f NL = 0,4 и 1 (но более подходящей выглядит модель с f NL = 1). Так как разрыв в K > 10 2 глубже, то одномерная модель с f NL = 1 дает нам гораздо меньшее Σ мин по сравнению с уравнением (10) (а двумерная симуляции). С другой стороны, Σ мин , полученные с помощью одномерной модели, согласуются с данными, полученными с помощью двумерного моделирования и уравнения (10). Для очень глубоких зазоров с K > 10 3 , Σ мин , заданное двумерным моделированием, меньше, чем предсказывает эмпирическая формула уравнения (10). {\infty}$|. Потребовалась бы более сложная модель возбуждения волн планетой-гигантом, чтобы воспроизвести глубину очень глубоких щелей с K > 10 4 .
{\infty}$|. Потребовалась бы более сложная модель возбуждения волн планетой-гигантом, чтобы воспроизвести глубину очень глубоких щелей с K > 10 4 .
Рис. 7.
Открыть в новой вкладкеСкачать слайд
(Слева) Минимальное значение азимутально осредненной поверхностной плотности Σ мин в зависимости от параметра K . Кружками обозначено значение Σ мин , полученное в результате двумерного моделирования Kanagawa et al. (2016). Пунктирной линией показано уравнение (10), а сплошной и штрих-пунктирной линиями показано Σ мин , полученное решением уравнения (12) с 9{\ prime } _ {\ min } $ | , как указано Kanagawa et al. (2016) (кружки). Крестики, квадраты и треугольники обозначают глубину разрыва, указанную Фунгом, Ши и Чангом (2014), Варньером, Куилленом и Франком (2004) и Даффеллом и Чиангом (2015) соответственно. (В цвете онлайн)
Эмпирическая формула уравнения (10) предсказывает большее значение Σ мин , чем значение, полученное в результате двумерного моделирования для K > 10 3 , как показано выше. {\prime }_{\min }$|, которая представляет собой поверхностную плотность, усредненную по всей области дна зазора, как Fung, Shi, and Chiang (2014) показал. 9{\ простое} _ {\ мин} $ | представляет собой поверхностную плотность около R = R p ± 2 R H , а не Σ мин = Σ( p ). Согласно Танигава и Ватанабэ (2002), скорость аккреции газа на планету зависит от поверхностной плотности вокруг места, которое в два раза больше радиуса Хилла, чем планета. Следовательно, уравнение (10) может быть полезным для оценки скорости аккреции газа, тогда как оно завышает минимальную поверхностную плотность щели при К ≳ 10 3 .
{\prime }_{\min }$|, которая представляет собой поверхностную плотность, усредненную по всей области дна зазора, как Fung, Shi, and Chiang (2014) показал. 9{\ простое} _ {\ мин} $ | представляет собой поверхностную плотность около R = R p ± 2 R H , а не Σ мин = Σ( p ). Согласно Танигава и Ватанабэ (2002), скорость аккреции газа на планету зависит от поверхностной плотности вокруг места, которое в два раза больше радиуса Хилла, чем планета. Следовательно, уравнение (10) может быть полезным для оценки скорости аккреции газа, тогда как оно завышает минимальную поверхностную плотность щели при К ≳ 10 3 .
5 Обсуждение
5.1 Применение наблюдений
5.1.1 Ограничение радиальной структуры зазора
Здесь мы хотели бы обсудить наблюдательные приложения нашей эмпирической формулы структуры зазора уравнения (6). Недавно с помощью ALMA было обнаружено много щелевых структур: они были обнаружены не только в пыли (например, ALMA Partnership et al. 2015), но и в газе (например, Yen et al. 2016). Такие щелевые структуры в протопланетных дисках могут создаваться за счет роста пыли (Чжан и др., 2015 г.), спекания (Окузуми и др., 2016 г.), эффектов МРТ (Флок и др., 2015 г.), вековой гравитационной нестабильности из-за газопылевого трения. (Takahashi & Inutsuka 2016) и взаимодействие диска с планетой. Трудно отличить происхождение от наблюдений. Однако, используя взаимосвязь радиальной структуры щели, показанную выше, мы можем оценить, обусловлена ли наблюдаемая щель взаимодействием диска и планеты.
Недавно с помощью ALMA было обнаружено много щелевых структур: они были обнаружены не только в пыли (например, ALMA Partnership et al. 2015), но и в газе (например, Yen et al. 2016). Такие щелевые структуры в протопланетных дисках могут создаваться за счет роста пыли (Чжан и др., 2015 г.), спекания (Окузуми и др., 2016 г.), эффектов МРТ (Флок и др., 2015 г.), вековой гравитационной нестабильности из-за газопылевого трения. (Takahashi & Inutsuka 2016) и взаимодействие диска с планетой. Трудно отличить происхождение от наблюдений. Однако, используя взаимосвязь радиальной структуры щели, показанную выше, мы можем оценить, обусловлена ли наблюдаемая щель взаимодействием диска и планеты.
Используя уравнение (5), мы можем определить отношение ширины зазора для любых двух произвольных поверхностных плотностей Σ th,a и Σ th,b как
\begin{eqnarray}
\frac{\Delta _{\rm gap}(\Sigma _{\rm th,a})}{\Delta _{\rm gap}(\Sigma _{\rm th,b})} = \frac{ \Sigma _{\rm th,a}/{\Sigma _0}+0,32}{\Sigma _{\rm th,b}/{\Sigma _0}+0,32}. \end{eqnarray}
\end{eqnarray}
(17)
Как видно из приведенного выше уравнения, отношение ширин зазоров зависит только от поверхностных плотностей, определяемых ширинами. На рисунке 8 показаны два отношения ширины зазора, определяемые как Σ th = 0,1Σ 0 и 0,5Σ 0 , а через Σ th = 0,3Σ 0 и 0,5Σ 0 . Используя уравнение (8), получаем отношения 0,51 и 0,76. Как видно из рисунка, соотношения, полученные в результате моделирования, достаточно хорошо согласуются с соотношениями, полученными с помощью уравнения (17).
Рис. 8.
Открыть в новой вкладкеСкачать слайд
Отношения ширины зазора, определяемые Σ th = 0,1Σ 0 , к значениям, определяемым Σ -й = 0,5Σ 0 (треугольники) и через Σ -й = 0,3Σ 0 и 0,5Σ 0 (крестики). Горизонтальные пунктирные линии указывают значения, предсказанные уравнением (17). (В цвете онлайн)
(В цвете онлайн)
5.1.2 Соотношение глубины и ширины зазора
Как показано в Kanagawa et al. (2016), существует зависимость между глубиной и шириной щели. Объединив уравнения (5) и (10), мы можем вывести это соотношение с точки зрения местоположения Σ th следующим образом: 9{-1/2}} \номер\\ &&{ \quad= 1,16\frac{\Sigma _{\rm th}}{\Sigma _0} + 0,35. } \end{eqnarray}
(18)
Если щель создана планетой, то ее ширина, измеренная плотностью над поверхностью, должна удовлетворять уравнению (18). Когда структура щели полностью решена и соотношение сторон диска точно оценено, мы можем использовать ширину щели, измеренную по разной поверхностной плотности на краю щели, и уравнение (18), чтобы строго судить о том, была ли щель создана планетой.
5.
 1.3 Применимость модели
1.3 Применимость моделиТеперь мы обсудим некоторые соображения, касающиеся применения уравнений (17) и (18) к наблюдениям, даже если наблюдаемый разрыв достаточно разрешен. Во-первых, мы должны учитывать, что распределение частиц пыли может отличаться от распределения газа, когда соотношения применяются к наблюдению за тепловым излучением пыли. Из-за фильтрации пыли (например, Zhu et al. 2012b; Dipierro et al. 2015; Picogna & Kley 2015; Rosotti et al. 2016) зазор в пыли может быть глубже и шире, чем зазор в газе, если размер частиц пыли (или число Стокса частиц) относительно велико. Следовательно, уравнения (17) и (18) следует использовать для наблюдений дискового газа. С другой стороны, взаимодействие пыли и газа зависит от поверхностной плотности газа, а также от размера частиц пыли. Если плотность газа достаточно велика, частицы газа и пыли будут хорошо перемешаны. В этом случае уравнения (17) и (18) дадут хорошую оценку.
Во-вторых, мы предполагаем, что щелевая структура находится в стационарном состоянии. Как показано в приложении 1, шкалу времени, необходимую для установления устойчивого состояния разрыва, можно приблизительно оценить как 91 523 t 91 524 90 283 по сравнению с 90 284 ∼ 0,1 млн лет. Если наблюдаемый разрыв моложе этой временной шкалы, он будет уже, чем разрыв, когда он находится в устойчивом состоянии. Такие молодые зазоры не могут быть оценены уравнениями (17) и (18).
Как показано в приложении 1, шкалу времени, необходимую для установления устойчивого состояния разрыва, можно приблизительно оценить как 91 523 t 91 524 90 283 по сравнению с 90 284 ∼ 0,1 млн лет. Если наблюдаемый разрыв моложе этой временной шкалы, он будет уже, чем разрыв, когда он находится в устойчивом состоянии. Такие молодые зазоры не могут быть оценены уравнениями (17) и (18).
Отметим, что уравнения (17) и (18) следует использовать для относительно глубоких зазоров. Как показано на рисунке 1, для неглубокого зазора ( K ΄ < 1), фактическая ширина зазора, измеренная для большей поверхностной плотности, несколько больше, чем оценка по уравнению (18). Из-за этого в данном случае уравнение (18) оценивает высоту шкалы диска примерно в 1,5 раза по сравнению с фактическим значением. Более того, как также обсуждалось в Kanagawa et al. (2016) следует учитывать наблюдательные неопределенности радиуса орбиты планеты и соотношения сторон.
Наконец, мы кратко комментируем наше предположение о двумерных дисках и пространственно постоянной кинематической вязкости ν. Фунг и Чианг (2016) выполнили трехмерное моделирование взаимодействия диска с планетой в случае, когда глубокая щель создается планетой. Профиль щели (т.е. глубина и ширина) не сильно отличается от результатов двумерных расчетов. Следовательно, наши модели могут быть действительными даже при правильном учете трехмерных эффектов. Предположение о постоянной вязкости может не всегда выполняться. Чжу, Стоун и Рафиков (2013) выполнили идеальное МГД-моделирование взаимодействия между маломассивной планетой и диском и показали, что эффективная вязкость α внутри зазора примерно в два раза больше, чем вне области зазора. Следовательно, зазор может быть меньше, чем в нашей модели. Однако, поскольку зависимость α от глубины зазора не очень сильная (см. уравнение (10)), этот эффект не может существенно повлиять на наши результаты.
Фунг и Чианг (2016) выполнили трехмерное моделирование взаимодействия диска с планетой в случае, когда глубокая щель создается планетой. Профиль щели (т.е. глубина и ширина) не сильно отличается от результатов двумерных расчетов. Следовательно, наши модели могут быть действительными даже при правильном учете трехмерных эффектов. Предположение о постоянной вязкости может не всегда выполняться. Чжу, Стоун и Рафиков (2013) выполнили идеальное МГД-моделирование взаимодействия между маломассивной планетой и диском и показали, что эффективная вязкость α внутри зазора примерно в два раза больше, чем вне области зазора. Следовательно, зазор может быть меньше, чем в нашей модели. Однако, поскольку зависимость α от глубины зазора не очень сильная (см. уравнение (10)), этот эффект не может существенно повлиять на наши результаты.
5.2 Возбуждение и распространение волн с глубокими зазорами
5.
 2.1 Планетарный крутящий момент и распределение углового момента в диске
2.1 Планетарный крутящий момент и распределение углового момента в дискеВ разделе 4 мы представляем эмпирическую модель распространения волн и получаем полуаналитическую одномерную модель структура зазора с использованием этой модели распространения волны. В предыдущих исследованиях (например, Goodman & Rafikov 2001), когда масса планеты была достаточно большой, как M p > M 1 (~1 × 10 9{-5/4}$|) из места рядом с точкой запуска. Однако наша модель распространения волн [уравнения (14), (15) и (16)] подразумевает, что распространение волн отличается от того, которое ожидается по модели Гудмана и Рафикова (2001), когда планета большая. Для лучшего понимания распространения волн с глубоким зазором мы обсудим, как меняются свойства распространения волн по мере увеличения массы планеты.
На рисунке 9 показан суммарный планетарный крутящий момент T p 9{\rm волна}$|, а кумулятивный крутящий момент T d , полученный с помощью двумерного гидродинамического моделирования, для небольшой планеты ( M p / M * -= 10 4 ), планета с умеренной массой ( M p / M * = 5 × 10 −4 ) и планета-гигант ( M p * = 10 −3 ). Соотношение сторон диска и вязкость 1/20 и 10 9{\rm волна}$|, пунктирная линия) и кумулятивный крутящий момент ( T d , пунктирная линия) для M p / M * −= 10 49015 (слева), 5 × 10 −4 (в центре) и 10 −3 (справа). Соотношение сторон диска и вязкость были установлены на 1/20 и 10 -3 соответственно. (Внизу) Усредненное по азимуту распределение поверхностной плотности в каждом случае. (В цвете онлайн)
Соотношение сторон диска и вязкость 1/20 и 10 9{\rm волна}$|, пунктирная линия) и кумулятивный крутящий момент ( T d , пунктирная линия) для M p / M * −= 10 49015 (слева), 5 × 10 −4 (в центре) и 10 −3 (справа). Соотношение сторон диска и вязкость были установлены на 1/20 и 10 -3 соответственно. (Внизу) Усредненное по азимуту распределение поверхностной плотности в каждом случае. (В цвете онлайн)
Когда M p / M 9{\ гт волна} $ | происходит намного медленнее, что указывает на то, что смещение углового момента волн становится менее эффективным по мере увеличения массы планеты. Вне разрыва поведение T p существенно отличается от такового в случае M p / M * = 10 −4 . Около R / R p = 1,5, T p уменьшается, а затем снова увеличивается около R / 9{\ гт волна} $ | медленнее, и увеличение T d тоже очень медленное.
5.2.2 Возбуждение и затухание волн в модах с низким m
Для дальнейшего изучения распространения волн при наличии глубокой щели мы исследуем волновые резонансы, связанные с малым волновым числом, используя результаты двумерного моделирования. Рассмотрим компоненты Фурье для Σ, v R , v ϕ и Ψ, которые задаются формулой
9{2\pi }_{0} f(R,\phi) \exp \left(-im\phi \right) d\phi, \end{eqnarray}(19)
, где f равно Σ, v R , v ϕ или Ψ. Для удобства пусть индекс m указывает на m -ю компоненту Фурье. Плотность крутящего момента, действующая на м -го резонанса, определяется выражением (Goldreich & Tremaine 1980)
\begin{eqnarray}
\left( \frac{dT_{\rm p}}{dR} \right)_m = 4\pi R \Re (\Psi _m) \Im (\Sigma _m),
\end{эквнаррай} 9{\ пм волна}. \end{eqnarray}
\end{eqnarray}
(23)
На рисунке 10 мы иллюстрируем совокупный крутящий момент, создаваемый планетой, и крутящий момент на диске для низких м мод. Параметры диска и планеты такие же, как на рисунке 9. Мы наносим вклады от m = 1–4 по отдельности и сумму вкладов от мод больше 4. В случае M p / M * = 10 −4 (левая часть рисунка), планетарный крутящий момент в основном создается резонансами с м > 4, так как возбуждение волны происходит в линейном режиме (Goldreich & Tremaine 1980). В кумулятивных крутящих моментах также преобладает вклад м > 4 волн.
Рис. 10.
Открыть в новой вкладкеСкачать слайд
Вклады совокупного планетарного крутящего момента (вверху) и кумулятивного вкладного крутящего момента (внизу) от азимутальных мод в тех же случаях, что и на рис. 9. Штриховая, сплошная, пунктирная, пунктирные и двойные штрихпунктирные линии обозначают вклады от м = 1, 2, 3, 4 и сумма м > 4 соответственно. Мы наносим только сумму 91 523 m 91 524 ≤ 4 (серая сплошная линия) и сумму 91 523 m 91 524 > 4, когда нижние азимутальные моды очень малы. (В цвете онлайн)
Мы наносим только сумму 91 523 m 91 524 ≤ 4 (серая сплошная линия) и сумму 91 523 m 91 524 > 4, когда нижние азимутальные моды очень малы. (В цвете онлайн)
В случаях, когда масса растений велика, как показано на средней и правой панелях рисунка 10, вклад небольших м резонанса значимы. Например, в случае M p / M * = 10 −3 (правая часть рисунка) вклад крутящего момента от резонансов 1 ≤ м ≤ 4 сравнимы с суммой вкладов от m > 4 резонансов. Вклады от m = 3, 4 резонансов возбуждаются вокруг края щели ( R / R p ≃ 1,2). Взносы от м = 1, 2 резонанса значительно возбуждаются вне щели. Изменение T p на больших расстояниях, указанное в предыдущем подразделе (и показанное на рисунке 9), происходит от вкладов m = 1, 2 резонансов. Отметим, что вклад м = 1 резонанса связан с косвенным членом гравитационного потенциала (который связан с гравитационным взаимодействием между планетой и центральной звездой), который как раз колеблется вокруг нуля на больших расстояниях от планеты, и вклад м = 1 не оказывает существенного влияния на поток углового момента волн.
Как показано в планетарном крутящем моменте, вклад кумулятивного крутящего момента от малых м мод становится больше по мере увеличения массы планеты. Когда м = 2, в частности, даже на очень далеких от планеты радиусах ( R / R p ∼ 2), совокупный вклад крутящего момента медленно увеличивается, в случае M стр. / M * = 10 −3 . Такое поведение T p и T d свидетельствует о том, что волны с малыми модами m (кроме m = 1) значительно возбуждают и переносят угловой момент на большие радиусы от планеты, с увеличение массы планеты. По мере того, как щель становится глубже и шире, вклады в возбуждение волн от крупных м резонансов (вблизи планеты) становятся меньше, поскольку поверхностная плотность в резонансе уменьшается. Вследствие этого волновое возбуждение на меньших м резонанса становится значительным, как обсуждалось Juhász et al. (2015). Более того, Lee (2016) показал, что возбуждение волн с малыми азимутальными волновыми числами может быть усилено за счет нелинейных эффектов. Значительное возбуждение волн с малыми м и м можно было бы объяснить раскрытием щели и нелинейными эффектами.
(2015). Более того, Lee (2016) показал, что возбуждение волн с малыми азимутальными волновыми числами может быть усилено за счет нелинейных эффектов. Значительное возбуждение волн с малыми м и м можно было бы объяснить раскрытием щели и нелинейными эффектами.
Следует отметить, что волна с м = 2 отдает угловой момент вне щели с Σ > Σ 0 ( R / R стр. > 1.8). Это указывает на то, что более широкий зазор образуется за счет выделения углового момента волны м = 2, тогда как для открытия такого широкого зазора требуется очень большое время, сравнимое со временем жизни диска [см. уравнение (3)] .
Развитие м = 1, 2 вклада существенно изменяет морфологию волн помимо переноса углового момента. На рисунке 11 мы показываем поверхностную плотность, создаваемую м = 1, 2 компонентов и суммой м > 2 компонентов, в том же случае, что и на рисунке 10. Поверхностная плотность, создаваемая м -м компонентом, равна
Поверхностная плотность, создаваемая м -м компонентом, равна
\begin{eqnarray} \Sigma (m,R,\phi ) = 2\pi \Sigma _m(R,\phi ) \exp \left(im\phi \right), \end{eqnarray}
(24)
где Σ m — фурье-компонента поверхностной плотности. Волны, находящиеся далеко от планеты, создаются вкладами м = 1 и м = 2 резонанса. В частности, вторичная волна, запускаемая с площадки, противоположной планете, в основном состоит из компонентов м = 1 и м = 2. Поскольку вклад компоненты м = 2 велик, вторичная волна зарождается в месте, противоположном планете. Фунг и Донг (2015) показали, что азимутальное разделение первичных и вторичных волн зависит от массы планеты. Для большой планеты, как показано на рисунке 11, это расстояние близко к 180°, что согласуется с нашими результатами. Для меньшей планеты расстояние меньше 180°. В этом случае вклады других низших мод (например, м = 3, 4), ненамного меньше, чем у м = 1, 2 (см. рис. 10). Из-за этих вкладов точка запуска вторичной волны будет двигаться к планете.
рис. 10). Из-за этих вкладов точка запуска вторичной волны будет двигаться к планете.
Fig. 11.
Open in new tabDownload slide
Two-dimensional surface density distribution in the case of M p / M * = 10 −3 , h / R p = 1/20, а α = 10 −3 . Показаны поверхностные плотности, создаваемые всеми модами (вверху слева), модами м > 2 (вверху справа), модой м = 1 (внизу слева) и модой м = 2 (внизу справа). . (в цвете онлайн)
Стоит отметить, что вторичная волна взаимодействует с планетой. Как видно на рисунке 11, вторичная волна проходит через точку, в которой ϕ = ϕ p вокруг R / R p = 1,4. Рядом с этим местом планетарный крутящий момент из-за м = 2 резонанс увеличивается, а затем уменьшается, как показано на верхней панели рисунка 10: это результат взаимодействия между планетой и вторичной волной. Кумулятивный крутящий момент м = 2 также увеличивается и уменьшается, когда вторичная волна проходит через место, в котором ϕ = ϕ p : это также является следствием взаимодействия между планетой и вторичной волной, и особенно м = 2 компонента.
Кумулятивный крутящий момент м = 2 также увеличивается и уменьшается, когда вторичная волна проходит через место, в котором ϕ = ϕ p : это также является следствием взаимодействия между планетой и вторичной волной, и особенно м = 2 компонента.
5.3 Эффекты неустойчивости щелевых конструкций
Предыдущие исследования (например, Ли и др., 2000; Танигава и Икома, 2007; Лин, 2012, 2014; Оно и др., 2014, 2016; Волновая нестабильность (RWI)] возникают на краю разрыва, вызванного планетой. Условие начала RI задается формулой d ( R 2 Ω)/ dR < 0 (Chandrasekhar 1961). Однако в нашем диапазоне параметров это условие не выполняется, поскольку структура щели менее крутая. Для очень глубокого разрыва с массивной планетой, где 92$| Для M P / M * = 10 −4 , 5 × 10 — 4 и 10 — 3 , когда H 3333333333333333.
343334333434343334343334333.
34333433343434333433343. . . 1/20 и α = 10 −3 . Когда M p / M * = 10 −4 и 5×10 −4 , экстремума вокруг края разрыва нет. Когда M p / M * = 10 −3 , мы можем найти локальный минимум и максимум около 92$| в случае M p / M * = 10 −3 на левой панели. (В цвете онлайн)
В случае низкой вязкости RWI может возникать на краю планетарного зазора (например, Ю и др., 2010; Фу и др., 2014; Чжу и др., 2014; см. также приложение 4). В этом случае RWI может ограничивать структуру разрыва, как утверждают Hallam and Paardekooper (2017). Однако при вязкости более α ~ 10 -3 -10 -4 , RWI стабилизируется вязкостью в течение долговременной эволюции (например, Lin 2014; Fu et al. 2014; Zhu & Stone 2014). . На самом деле нет четких доказательств того, что RWI влияет на структуру разрыва на рисунке 12. В этом случае влияние RWI на структуру разрыва может быть несущественным.
2014; Zhu & Stone 2014). . На самом деле нет четких доказательств того, что RWI влияет на структуру разрыва на рисунке 12. В этом случае влияние RWI на структуру разрыва может быть несущественным.
6 Резюме
Используя результаты обзора гидродинамического моделирования (34 прогона) в широком пространстве параметров, мы получили количественную связь между планетой и радиальной структурой щели. Мы также получаем эмпирическую модель распространения волн по результатам опроса. Применяя эту эмпирическую модель распространения волн к полуаналитической модели структуры зазора, представленной в K15, мы можем получить структуры зазоров, которые очень хорошо согласуются с полученными при двумерном моделировании. Наши результаты можно резюмировать следующим образом:
Мы расширили масштабное соотношение ширины зазора, данное Kanagawa et al. (2016). Из этого масштабного соотношения мы получили эмпирическую формулу для распределения поверхностной плотности зазора [уравнение (6)], которая точно воспроизводит результаты гидродинамического моделирования (см.
 рисунок 2).
рисунок 2).Наша модель накладывает ограничение на происхождение наблюдаемой структуры разрыва, как обсуждалось в подразделе 5.1. Используя уравнения (17) и (18), мы можем судить, вызван ли наблюдаемый разрыв планетой (см. рисунок 8).
Мы подтвердили правильность эмпирической модели распространения волн, принятой в K15 [уравнение (14)] с параметрами, заданными уравнениями (15) и (16). Эта модель описывает распространение волн, которое согласуется с результатами гидродинамического моделирования (см. рисунок 5). Используя эту модель распространения волны, мы можем воспроизвести структуру зазора, полученную в результате двумерного гидродинамического моделирования с использованием одномерной модели (см. рисунок 6).
Наша модель распространения волн показывает, что волны, возбуждаемые большей планетой, переносят угловой момент на большие расстояния от планеты. Чем больше масса планеты, тем сильнее возбуждаются волны с меньшим азимутальным волновым числом (например, 91 523 м 91 524 = 2).
 Угловой момент переносится в отдаленные места от планеты, даже если масса планеты больше массы Юпитера (см. рисунок 10).
Угловой момент переносится в отдаленные места от планеты, даже если масса планеты больше массы Юпитера (см. рисунок 10).Развитие мод с малыми азимутальными волновыми числами изменяет морфологию спиральных волн. Когда масса планеты достаточно велика, м = 2 мода создает вторичную волну, запускаемую с противоположной от планеты площадки (см. рисунок 11), в дополнение к первичной волне, исходящей из расположения планеты. Вторичная волна будет тесно связана с переносом углового момента.
С увеличением массы планеты нелинейные эффекты становятся существенными в возбуждении и распространении волн, и поэтому механизм образования щели отличается от того, когда планета мала в линейной теории. Однако эти теоретические механизмы еще не до конца поняты. Чтобы понять механизм образования щели и морфологию волн плотности, индуцированных планетой-гигантом, необходимо будет дополнительно исследовать возбуждение и распространение волн при наличии глубоких щелей.
Благодарности
Эта работа была поддержана грантами JSPS KAKENHI №№ 23103004, 26103701, 26800106 и 26800229, а также грантом Польского национального научного центра MAESTRO DEC-2012/06/A/ST9/00276. KDK был поддержан исследовательским грантом ALMA Japan Чилийской обсерватории NAOJ, NAOJ-ALMA-0135. Численные расчеты проводились на Cray XC30 в Центре вычислительной астрофизики Национальной астрономической обсерватории Японии и Пан-Охотской информационной системе Института наук о низких температурах Университета Хоккайдо.
Приложение 1. Изменение глубины и ширины щелей во времени
Здесь мы рассматриваем изменение во времени глубины и ширины щелей. На рисунке 13 показано изменение во времени ширины и глубины зазора (слева) и моментальный снимок азимутально усредненной поверхностной плотности (справа) для M p / M * = 10 −3 , α = 10 −3 и h p / R p = 1/25. Сначала рассмотрим изменение ширины щели во времени. Как видно на левой панели рисунка 13, узкий зазор Δ зазор = 0,4 R p , образуется на t = 100 планетарных орбит. Ширина щели постепенно увеличивается со временем. Наконец, ширина зазора достигает 0,79 R p при t ≃ t vis = 1,5 × 10 4 планетарных орбит. После этого ширина зазора почти насыщается. Распределение усредненной по азимуту поверхностной плотности со временем становится шире, как показано на правом графике. Отметим, что эволюция поверхностной плотности несколько асимметрична относительно планеты: это может быть связано с влиянием внутренней границы. Однако структура разрыва почти симметрична, как видно на правой панели.
Сначала рассмотрим изменение ширины щели во времени. Как видно на левой панели рисунка 13, узкий зазор Δ зазор = 0,4 R p , образуется на t = 100 планетарных орбит. Ширина щели постепенно увеличивается со временем. Наконец, ширина зазора достигает 0,79 R p при t ≃ t vis = 1,5 × 10 4 планетарных орбит. После этого ширина зазора почти насыщается. Распределение усредненной по азимуту поверхностной плотности со временем становится шире, как показано на правом графике. Отметим, что эволюция поверхностной плотности несколько асимметрична относительно планеты: это может быть связано с влиянием внутренней границы. Однако структура разрыва почти симметрична, как видно на правой панели.
Рис. 13.
Открыть в новой вкладкеСкачать слайд M p / M * = 10 −3 . (Слева) Изменение во времени ширины зазора, измеренной с помощью Σ th = 0,5Σ 0 (сплошная линия), и поверхностной плотности, усредненной по дну зазора (см. текст; пунктирная линия). (Справа) Радиальное распределение азимутально усредненной поверхностной плотности на t = 800 (штриховая линия), 2000 (пунктирная линия) и 20000 (сплошная линия) оборотов планеты. (В цвете онлайн)
текст; пунктирная линия). (Справа) Радиальное распределение азимутально усредненной поверхностной плотности на t = 800 (штриховая линия), 2000 (пунктирная линия) и 20000 (сплошная линия) оборотов планеты. (В цвете онлайн)
На рисунке 14 показаны изменения ширины и глубины зазора во времени для случаев с различной вязкостью. Ширина зазора насыщается медленнее при меньшей вязкости, как и ожидалось из уравнения (4). В обоих случаях на рисунке после 91 523 t 91 524 ≃ 91 523 t 91 524 90 283 vis 90 284 ширины зазоров насыщаются. Время насыщения глубины зазора также зависит от вязкости. Если α = 10 −4 (правая панель рисунка 14), глубина щели насыщается после 10 4 витков, что примерно в 10 раз больше, чем в случае α = 10 −3 (средняя панель). Следовательно, если вязкость очень мала, требуется долгосрочное моделирование для получения зазоров в установившемся режиме.
Рис. 14.
Открыть в новой вкладкеСкачать слайд ). На левой панели α = 4 × 10 −3 , M p / M * = 10 −3 ; на средней панели α = 10 −3 , M p / M * = 10 −3 ; а на правой панели α = 10 −4 , M p / M * = 5 × 10 −4 . Соотношение сторон диска установлено на 1/20.
Соотношение сторон диска установлено на 1/20.
Приложение 2. Сравнение ширины зазора с предыдущими работами
Мы сравнили наши результаты с результатами гидродинамического моделирования в предыдущих исследованиях. На рисунке 15 показана ширина зазора, полученная в результате нашего моделирования, а также расчетов Варньера, Куиллена и Франка (2004 г.) и Даффелла и Макфадьена (2013 г.). Поскольку в этих исследованиях использовалось Σ th = (1/3)Σ 0 , чтобы определить ширину зазора, мы наносим ширину зазора, измеренную с помощью Σ th = (1/3)Σ 0 . 2 Для K ΄ ≲ 10 ширина зазора, полученная в предыдущих исследованиях, увеличивается как K ΄ 1/4 , что согласуется с результатами уравнения (5). Поскольку K ΄ продолжает увеличиваться, ширина щели, полученная в предыдущих исследованиях, имеет больший разброс по сравнению с нашими результатами. В частности, значения ширины, данные Duffell and MacFadyen (2013), значительно уже наших результатов. В основном они исследовали ситуации с очень низкой вязкостью, то есть α ≲ 10 −4 . Здесь мы напоминаем читателю об изменениях ширины зазора во времени, описанных в приложении 1. Время, необходимое для достижения зазором насыщенной ширины, оценивается по шкале вязкого времени, как в уравнении (3). Когда α = 10 −4 , шкала времени составляет около 10 5 орбит, хотя предыдущие исследования оценивали это в несколько тысяч планетарных орбит. Разница в ширине зазора, наблюдаемая в предыдущих исследованиях, может быть объяснена их коротким временем вычислений. Обратите внимание, что когда вязкость очень низкая, поскольку временная шкала уравнения (3) очень велика, зазор не может достичь насыщенной ширины в течение срока службы диска. В этом случае уравнение (5) занижает массу планеты.
В частности, значения ширины, данные Duffell and MacFadyen (2013), значительно уже наших результатов. В основном они исследовали ситуации с очень низкой вязкостью, то есть α ≲ 10 −4 . Здесь мы напоминаем читателю об изменениях ширины зазора во времени, описанных в приложении 1. Время, необходимое для достижения зазором насыщенной ширины, оценивается по шкале вязкого времени, как в уравнении (3). Когда α = 10 −4 , шкала времени составляет около 10 5 орбит, хотя предыдущие исследования оценивали это в несколько тысяч планетарных орбит. Разница в ширине зазора, наблюдаемая в предыдущих исследованиях, может быть объяснена их коротким временем вычислений. Обратите внимание, что когда вязкость очень низкая, поскольку временная шкала уравнения (3) очень велика, зазор не может достичь насыщенной ширины в течение срока службы диска. В этом случае уравнение (5) занижает массу планеты.
Рис. 15.
Открыть в новой вкладкеСкачать слайд
Ширина зазора с Σ th = (1/3)Σ 0 , полученная путем моделирования, проведенного Kanagawa et al. (2016) (кружки) и ширину зазора, указанную Duffell and MacFadyen (2013) (треугольники) и Varnière, Quillen, and Frank (2004) (квадраты). Тонкая линия указывает на решение уравнения (5) с Σ th = (1/3)Σ 0 . (В цвете онлайн)
(2016) (кружки) и ширину зазора, указанную Duffell and MacFadyen (2013) (треугольники) и Varnière, Quillen, and Frank (2004) (квадраты). Тонкая линия указывает на решение уравнения (5) с Σ th = (1/3)Σ 0 . (В цвете онлайн)
Даффелл и Чианг (2015) исследовали ширину зазора в вязком случае (α ∼ 10 −3 ). They measured the gap width using Σ th = 0.1Σ 0 and derived the following empirical formula: Δ gap / R p = 0.5( h p / R p ) 0,22 К ΄ 0,22 . Их эмпирическая формула очень похожа на уравнение (5), если ч p / R p = 0,04: это потому, что они в основном рассматривали случаи, когда ч р / Р р ≃ 0,04.
Приложение 3. Описание модели
C1 Распространение волн в одномерной модели
Для того чтобы связать двумерное моделирование с одномерной моделью К15, получаем выражение для распространения волн, которое задается в двумерной модели. размерное моделирование для полуаналитической модели. Мы использовали основные уравнения для двумерного гидродинамического моделирования, чтобы вывести основное уравнение для одномерной модели. 92 \ frac {\ partial \ Sigma } {\ partial \ phi} — \ Sigma \ frac {\ partial \ Psi } {\ partial \ phi} + R f _ {\ phi}.}
\end{eqnarray}
размерное моделирование для полуаналитической модели. Мы использовали основные уравнения для двумерного гидродинамического моделирования, чтобы вывести основное уравнение для одномерной модели. 92 \ frac {\ partial \ Sigma } {\ partial \ phi} — \ Sigma \ frac {\ partial \ Psi } {\ partial \ phi} + R f _ {\ phi}.}
\end{eqnarray}
(A1)
Гравитационный потенциал равен Ψ, а f ϕ — сила вязкости, действующая на единицу площади. Предполагалось, что фоновая структура осесимметрична и вращается с постоянной угловой скоростью, а возмущенная структура (волна) неосесимметрична и вращается с угловой скоростью, зависящей от R и ϕ. Следовательно, мы можем разложить азимутальную скорость на две части: фон и возмущение (Муто и др. 2010): 9{\rm avg}(R) + \delta {v}_{\phi}(R,\phi). \end{eqnarray}
(A2)
Обратите внимание, что уравнение (A2) не является линейным приближением. Усредненная по азимуту версия уравнения (A1) может быть записана как
Усредненная по азимуту версия уравнения (A1) может быть записана как
\begin{eqnarray} \ frac {\ partial R \ overline {\ Sigma {v} _ {\ phi}}} {\ partial t} + \ frac {1} {2 \ pi R} \ frac {\ partial F _ {\ rm J}} {\partial R}= — \frac{1}{2\pi R} \frac{dT _{\rm p}}{dR} , \end{eqnarray}
(A3)
где F J — осредненный по азимуту поток углового момента, 9{\ гт вис} $ | в уравнении (A6). Правая часть уравнения (A3) представляет гравитационный момент, возбуждаемый планетой. Азимутально усредненный поток массы, обозначаемый F M , определяется как |$\overline{\Sigma {v}_{R}}$|. Плотность крутящего момента в правой части уравнения (A3) получается следующим образом:
\begin{eqnarray} \frac{dT_{\rm p}}{dR} = 2 \pi R \overline{ \Sigma \frac{{\partial \Psi}}{\partial \phi}}, \end{eqnarray}
(A7)
9{R}_{R_{\rm p}} \overline{ \Sigma \frac{\partial \Psi }{\partial \phi}} RdR. \end{eqnarray}
\end{eqnarray}(A8)
Обратите внимание, что момент давления в Crida, Morbidelli, and Masset (2006) определяется усреднением первого члена в правой части уравнения (A1) вместе с линиями тока. Однако, поскольку мы усреднили уравнение (A1) по азимуту, этот член исчезает. Вместо момента давления мы рассматриваем поток углового момента, обусловленный волнами, описываемыми уравнением (A5). Чтобы прояснить влияние распространения волны, уравнение (A3) можно переписать как 9{\rm волна}}{dR} \право). \end{eqnarray}
(A9)
Во-первых, планета возбуждает волны и, таким образом, передает им угловой момент. Затем этот угловой момент передается на диск по мере затухания волн. Из-за распространения этой волны скорость передачи углового момента газу диска отличается от плотности крутящего момента, возбуждаемой планетой. Скорость осаждения волн определяется выражением
\begin{eqnarray}
\Lambda _{\rm d}(R) = \frac{dT _{\rm p}}{dR} — \frac{dF _{\rm J}^{\rm волна}}{dR}. \end{эквнаррай} 9{\rm волна}(R).
\end{эквнаррай} 9{\rm волна}(R).
Рис. 16 = 5 × 10 −4 и 10 −3 ( h p / R p = 1/20 и α = 10 −3 ). Толстые пунктирные линии представляют собой усредненный по азимуту поток, полученный по уравнению (A6), а тонкие сплошные линии представляют собой усредненный по азимуту поток, полученный только по первому члену уравнения (A6). (В цвете онлайн) 9{\ rm vis} (R) = F _ {\ rm J} (R _ {\ rm p}) + T _ {\ rm d} (R), \end{eqnarray}
(A13)
, что совпадает с основным уравнением [уравнение (9)] K15.
C2 Модель волнового возбуждения
В полуаналитической модели мы принимаем формулу ВКБ для плотности планетарного крутящего момента (например, Ward 1986) и используем простую отсечку, как в K15:
\begin{eqnarray}
\ frac {dT _ {\ rm p}} {dR} & = \ left \ lbrace \ begin {array} {ll} \, \ pm \, 0,40 f _ {\ rm NL} {\ displaystyle \ frac {\ Sigma (R )}{\Sigma _0} \left( \frac{h_{\rm p}}{RR _{\rm p}} \right)^{4} \left( \frac{dT _{\rm p}} {dR} \right)_0}\номер\\
\phantom{00000000000000000000000} \mbox{for} |RR_{\rm p}| > \Дельта,\\
0 \phantom{00000000000000000000000}\mbox{for} |RR_{\rm p}| \le \Delta , \end{массив}\right. \номер\\
\end{эквнаррай} 9{-4}.
\end{eqnarray}
\номер\\
\end{эквнаррай} 9{-4}.
\end{eqnarray}
(A15)
Для знака ± в уравнении (A14) + принимается за R > R p , а − берется за R 2 3 R 2 4 915 . Длина отсечки Δ должна быть установлена равной 1,3 ч p , чтобы соответствовать одностороннему крутящему моменту, полученному из линейного анализа взаимодействия диска с планетой (Такеучи и Мияма, 1998; Танака и др., 2002; Муто и Инуцука, 2009). Фактор f NL 93$| параметр K выражается как l 2 h p /α. Когда l > 1, K > h p /α. В искомом пространстве параметров (1/30 < h p / R p < 1/15, 10 −4 < α < 10 −2 ) возбуждение волн нелинейно когда K ∼ 10 2 . Хотя переход от линейного режима к нелинейному должен быть плавным, ступенчатая функция 9{\ infty} $ | зависит от поверхностной плотности, как видно из уравнения (A17). Следовательно, когда мы решаем уравнение (A13), необходима итерация, чтобы последовательно получить Σ и Λ d (или T d ). Подробнее см. в подразделе 2.4 в K15.
Следовательно, когда мы решаем уравнение (A13), необходима итерация, чтобы последовательно получить Σ и Λ d (или T d ). Подробнее см. в подразделе 2.4 в K15.
Приложение 4. Условия неустойчивости волны Россби в случае малой вязкости
Ono et al. (2016) получили необходимое и достаточное условие возникновения РВИ для различных структур в невязком случае. Они получили пороговую минимальную поверхностную плотность, когда RWI маргинально стабилен, в зависимости от ширины структур. Чтобы обсудить RWI в промежутке, мы сравним отношения пороговой минимальной плотности и ширины для структур гауссовой щели (GG) и ступенчатого скачка (SJU) (которые приблизительно моделируют структуру щели вне планетарной орбиты) с отношение глубины к ширине зазора, определяемое уравнением (18). Согласно Оно и соавт. (2016), пороговая минимальная плотность РВИ получается как Σ мин /Σ 0 | , где даются 93. 1 и 2.31 для ГГ, а 108.6 и 3.06 для конструкции СЖУ. 3 Если глубина зазора меньше, чем пороговая минимальная поверхностная плотность RWI, вихрь будет формироваться RWI. Обратите внимание, что Оно и соавт. (2016) исследовали RWI в относительно узких промежутках (Δ/ R p < 0,2), так как RWI стабилизируется в широкой щели как ≫ h p . Хотя мы применяем формулу Оно к широкому зазору, RWI может быть стабильным, даже если минимальная плотность зазора меньше, чем пороговая плотность, заданная их критерием, когда Δ/ R p велико. На рисунке 17 мы показываем отношение глубины к ширине зазора, принятое Σ th = 0,5 Σ 0 , и пороговое значение минимальной поверхностной плотности RWI для функции GG и SJU. Как показано на рисунке, RWI может произойти в промежутке, вызванном планетой, если вязкость очень низкая, что согласуется с предыдущими исследованиями (например, Yu et al. 2010; Fu et al. 2014; Zhu et al.
1 и 2.31 для ГГ, а 108.6 и 3.06 для конструкции СЖУ. 3 Если глубина зазора меньше, чем пороговая минимальная поверхностная плотность RWI, вихрь будет формироваться RWI. Обратите внимание, что Оно и соавт. (2016) исследовали RWI в относительно узких промежутках (Δ/ R p < 0,2), так как RWI стабилизируется в широкой щели как ≫ h p . Хотя мы применяем формулу Оно к широкому зазору, RWI может быть стабильным, даже если минимальная плотность зазора меньше, чем пороговая плотность, заданная их критерием, когда Δ/ R p велико. На рисунке 17 мы показываем отношение глубины к ширине зазора, принятое Σ th = 0,5 Σ 0 , и пороговое значение минимальной поверхностной плотности RWI для функции GG и SJU. Как показано на рисунке, RWI может произойти в промежутке, вызванном планетой, если вязкость очень низкая, что согласуется с предыдущими исследованиями (например, Yu et al. 2010; Fu et al. 2014; Zhu et al. 2014). Если возникает RWI, структура разрыва в устойчивом состоянии может определяться предельным состоянием RWI. В этом случае отношение глубины к ширине зазора можно определить по критерию Оно, а не по нашему соотношению в уравнении (18).
2014). Если возникает RWI, структура разрыва в устойчивом состоянии может определяться предельным состоянием RWI. В этом случае отношение глубины к ширине зазора можно определить по критерию Оно, а не по нашему соотношению в уравнении (18).
Рис. 17.
Открыть в новом слайде с нагрузкой
Глубина пробела и пополнения. = 1/20 (сплошная линия), 1/30 (пунктирная линия) и 1/15 (пунктирная линия). Вертикальная и горизонтальная оси указывают минимальную поверхностную плотность зазора и полную ширину зазора соответственно. В закрашенной серой области RWI нестабилен в случае структуры SJU. (В цвете онлайн)
1
The surface density is averaged over the annulus spanning R = R p − δ to R p + δ with δ ≡ 2max(R H , R p ) , вырезанный из θ = θ p − δ/ R p до θ p + δ/ R p . Эта плотность аналогична плотности дна щели, которую использовали Fung, Shi, and Chiang (2014) (мы не брали среднюю по времени плотность).
Эта плотность аналогична плотности дна щели, которую использовали Fung, Shi, and Chiang (2014) (мы не брали среднюю по времени плотность).
2
Строго говоря, Varnière, Quillen, and Frank (2004) приняли Σ th = 0,4 Σ 0 .
3
Оно и др. (2016) принял параметр A вместо Σ мин / Σ 0 . Используя параметр A, Σ мин /Σ 0 = 1/(1 + A ). В случае структуры SJU мы корректируем значение параметра a из таблицы 2 Ono et al. (2016), поскольку мы рассматриваем пороговую минимальную плотность как функцию полной ширины щели [Ono et al. (2016) рассматривали пороговую плотность как функцию полуширины щели (=Δ/2)].
Ссылки
Akiyama
E.
и др.
2015
,
APJ
,
802
,
L17
Akiyama
E.
et al.
2016
,
AJ
,
152
,
222
ALMA
Partnership
,
2015
,
ApJ
,
808
,
L3
Artymowicz
P.
,
Lubow
S. H.
1994
,
ApJ
,
421
,
651
Baruteau
C.
,
Meru
F.
,
Paardekooper
S.-J.
2011
,
МПР
,
416
,
1971
Бенисти
М.
и др.
2015
,
A & A
,
578
,
L6
Burke
C. J.
et al.
2014
,
APJS
,
210
,
19
Cameron
A. G. W.
1978
,
MOON и Planets
,
MOON и Planets
3
,
MOON и Planets
,
,
.0003
18
,
5
Chandrasekhar
S.
1961
,
Hydrodynamic and Hydromagnetic Stability
(
Oxford
:
Clarendon Press
)
Christiaens
V .
,
Casassus
S.
,
Perez
S.
,
Van der Plas
G.
,
0002 Ménard
F.
2014
,
ApJ
,
785
,
L12
Crida
A.
,
Morbidelli
A.
2007
,
MNRAS
,
377
,
1324
CRIDA
A.
,
Morbidelli
,
F.
,
F.
,
,
.0002 2006
,
Icarus
,
181
,
587
Currie
T.
,
Cloutier
R.
,
Brittain
S.
,
Grady
C.
,
Burrows
A.
,
Muto
T.
,
Kenyon
S. J.
,
Kenyon
S. J.
J.
,
Kenyon
S. J.
,
S. J.
,
S.0003M. J.
2015
,
ApJ
,
814
,
L27
Dipierro
G.
,
Price
D.
,
Laibe
G .
,
Hirsh
K.
,
Cerioli
A.
,
Lodato
G.
2015
,
MNRAS
,
453
,
L73
Dong
R.
,
Rafikov
R. R.
,
Stone
J. M.
2011
,
ApJ
,
741
,
57
Duffell
P. C.
2015
,
ApJ
,
807
,
L11
Duffell
P. C.
,
Chiang
E.
2015
,
ApJ
,
812
,
94
Duffell
P. C.
,
MacFadyen
A. I.
2013
,
APJ
,
769
,
41
Flock
M.
,
Ruge
J. P.
,
DZYUR0003
N.
,
Henning
T.
,
Klahr
H.
,
Wolf
S.
2015
,
A&A
,
574
,
A68
Fu
W.
,
Li
H.
,
Lubow
S.
,
Li
S.
2014
,
ApJ
,
788
,
L41
Fung
J.
,
Chiang
E.
2016
,
ApJ
,
832
,
105
Fung
J.
,
Dong
R.
2015
,
ApJ
,
815
,
L21
Fung
Дж.
,
Ши
Дж.-М.
,
Chiang
E.
2014
,
ApJ
,
782
,
88
Goldreich
P.
,
Tremaine
S.
1980
,
ApJ
,
241
,
425
Goodman
3
3 Дж.
30002 Rafikov
R. R.
2001
,
APJ
,
552
,
793
Grady
C. A.
et.
2013
,
APJ
,
762
,
48
Hallam
P. D.
,
Paardekooper
S.-J.-J.
2017
,
МИР РАН
,
469
,
3813
Ida
S.
,
Lin
D. N. C.
,
Nagasawa
M.
2013
,
ApJ
,
775
,
42
Juhász
A.
,
Benisty
M.
,
Pohl
A.
,
Dullemond
C. P.
,
Доминик
К.
,
Паардекупер
С.-Дж.
2015
,
MNRAS
,
451
,
1147
Kanagawa
K. D.
,
Fujimoto
M. Y.
Y.
2013
,
ApJ
,
765
,
33
Канагава
К. Д.
,
Muto
T.
,
Tanaka
H.
,
Tanigawa
T.
,
Takeuchi
T.
,
Tsukagoshi
T.
,
Momose
M.
2015a
,
ApJ
,
806
,
L15
Kanagawa
K. D.
,
Muto
T.
,
Tanaka
H.
,
Tanigawa
T.
,
Takeuchi
T.
,
Tsukagoshi
T.
,
Momose
M.
2016
,
PASJ
,
68
,
43
Kanagawa
K. D.
,
Tanaka
H.
,
Tanaka
H.
,
9000.,
9000.,
.0003
T.
,
Tanigawa
T.
,
Takeuchi
T.
2015b
,
MNRAS
,
448
,
994
Kley
В.
1999
,
МНРАС
,
303
,
696
2 Ли
2016
,
АпЖ
,
832
,
166
Li
H.
,
Finn
J. M.
,
Lovelace
R. V. E.
,
Colgate
S. A.
2000
,
ApJ
,
533
,
1023
Lin
D. N. C.
,
Papaloizou
J.
1979
,
MNRAS
,
186
,
799
Лин
М. -К.
-К.
2012
,
АпЖ
,
754
,
21
Лин
М.-К.
2014
,
MNRAS
,
437
,
575
Lovelace
R. V. E.
,
Li
H.
,
Colgate
S. A.
,
Nelson
A. F.
1999
,
ApJ
,
513
,
805
Lynden-Bell
D.
,
Pringle
J. E.
1974
,
MNRAS
,
168
,
603
Masset
F.
2000
,
A&AS
,
141
,
165
Miyoshi
K.
,
Takeuchi
T.
,
Tanaka
H.
,
Ida
S.
1999
,
APJ
,
516
,
451
Mizuno
H.
1980
,
PROG. Теор. физ.
,
64
,
544
Момосе
М.
и др.
2015
,
PASJ
,
67
,
83
Mordasini
C.
,
Alibert
Y.
,
Benz
W.
,
Klahr
H.
,
Henning
T.
2012
,
A&A
,
541
,
А97
Муто
Т.
и др.
2012
,
ApJ
,
748
,
L22
Muto
T.
,
Inutsuka
S.
2009
,
ApJ
,
701
,
18
Муто
т.
,
Suzuki
T. K.
,
INUTSUKA
S.
2010
,
APJ
,
724
,
9002 448 9000..1023.1023.1023.1023.10239000.10239000.2016
,
ApJ
,
819
,
L7
Okuzumi
S.
,
Momose
M.
,
Sirono
S.
,
Kobayashi
H.
,
Tanaka
H.
2016
,
ApJ
,
821
,
82
Ono
T.
,
Muto
T.
,
Takeuchi
T.
,
Nomura
H.
2016
,
ApJ
,
823
,
84
Ono
T.
,
Nomura
H.
,
Takeuchi
T.
2014
,
ApJ
,
787
,
37
Осорио
М.
и др.
2014
,
АпЖ
,
791
,
Л36
Петрович
C.
,
Rafikov
R. R.
2012
,
ApJ
,
758
,
33
Picogna
G.
,
Kley
W.
2015
,
A & A
,
584
,
A110
Rafikov
R.
2002
,
APJ1103
,
APJ
1103
.0002 569
,
997
Rosotti
G. P.
,
Juhasz
A.
,
Booth
R. A.
,
Clarke
C. J.
2016
,
MNRAS
,
459
,
2790
Sallum
S.
и др.
2015
,
Природа
,
527
,
342
Shakura
N. I.
,
Sunyaev
R. A.
1973
,
AAP
,
24
,
337
Takahashi
S. Z.
,
INUTSUKA
S.
2016
,
AJ
,
152
,
184
Takeuchi
,
184
Takeuchi
0002 T.,
Miyama
S. M.
1998
,
PASJ
,
50
,
141
Takeuchi
T.
,
Miyama
S. M.
,
LIN
D. N. C.
1996
,
APJ
,
460
,
832
Tanaka
H.
,
H.
H.
T.
,
Ward
W. R.
2002
,
ApJ
,
565
,
1257
Tanigawa
T.
,
Ikoma
M.
2007
,
APJ
,
667
,
557
Tanigawa
T.
,
Watanabe
S.
,
Watanabe
S.
,
Watanabe 9000
S.
,
S.
,
S.
,
T.
,
.0002 2002
,
ApJ
,
580
,
506
Цукагоши 910 Tal
2016
,
APJ
,
829
,
L35
Van Der Marel
N.
,
Van Dishoeck
. F.
,
Van Dishoeck
. F.
,
,
92.110,9000.
,
.
,
Эндрюс
С. М.
,
Pontoppidan
K. M.
M.
,
Herczeg
G. J.
,
van Kempen
T.
,
Miotello
A.
2016
,
A&A
,
585
,
A58
Varnière
P.
,
Quillen
A. C.
,
Frank
A.
2004
,
Frank
A.
2004
,
Frank
A.
2004
,
A.
2004
,
.0003
,
ApJ
,
612
,
1152
Ward
W. R.
R.
1986
,
Icarus
,
67
,
164
Yen
Х.-В.
,
Лю
Х.Б.
,
Гу
П.-Г.
,
Хирано
Н.
,
Ли
К.-Ф.
,
Puspitaningrum
E.
,
Takakuwa
S.
2016
,
ApJ
,
820
,
L25
Yu
C.
,
LI
H.
,
LI
S.
,
Lubow
S. H.
,
LIN
D. N. C.
2010
,
D. N. C.2010
,
9000D. N. C.
2010
,
9000ApJ
,
712
,
198
Zhang
K.
,
Blake
G. A.
,
Bergin
E. A.
2015
,
ApJ
,
806
,
L7
Zhu
Z.
,
Hartmann
L.
,
Nelson
R. P.
P.
,
R. P.
,
0002 Gammie
C. F.
2012a
,
ApJ
,
746
,
110
Zhu
Z.
,
Nelson
R. P.
,
Dong
R.
,
Espaillat
C.
,
Hartmann
L.
2012b
,
ApJ
,
755
,
6
Zhu
Z.
,
Nelson
R. P.
,
Hartmann
L.
,
Espaillat
C.
,
Calvet
N.
2011
,
APJ
,
729
,
47
Zhu
Z.
,
J. M.
2014
10,J. M.
2014
,
J. M.
2014
10,J. M.
2014
10,J. M.
2014 9000.
,
.0002 APJ
,
795
,
53
Zhu
Z.
,
J. M.
,
RAFIK. ,
768
,
143
Zhu
Z.
,
Камень
J. M.
,
Рафикова
R.
,
0002 Бай
Х.-Н.
2014
,
ApJ
,
785
,
122
© The Author, 2017. Опубликовано Японским астрономическим обществом. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected]
© Автор, 2017 г. Опубликовано Oxford University Press от имени Астрономического общества Японии. Все права защищены. Чтобы получить разрешения, отправьте электронное письмо по адресу: [email protected]
Тема
аккреция, аккреционные дискипланеты и спутники: формированиепротопланетные дискивзаимодействия планета-диск
Выпускной раздел:
Бумага
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о теме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Система астрофизических данных
Резюме объявленийСсылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Широкое и глубокое исследование радиогалактик с помощью Subaru HSC (WERGS). IX. Наиболее плотная область на z ∼ 5, населенная массивной радиогалактикой
IX. Наиболее плотная область на z ∼ 5, населенная массивной радиогалактикой
Данные Gaia DR2 и EDR3 и эволюционный статус звезд post-AGB с высокими лучевыми скоростями
Трио планет-гигантов, вращающихся вокруг эволюционировавшей звезды HD 184010
.Калибровка поляризации тандемного эталонного магнитографа Телескопа исследования солнечной магнитной активности в обсерватории Хида
PNV J00444033+4113068: Ранние сверхгорбы с амплитудой 0,7 величины и некрасным цветом
Реклама
Что такое конфокальная микроскопия с вращающимся диском?
Введение
Типичная флуоресцентная микроскопия включает освещение всего образца и обнаружение результирующей флуоресценции. Освещение и обнаружение всего образца включает в себя сбор расфокусированного света выше и ниже фокальной плоскости, что приводит к размытости и ухудшению качества изображения. Этот эффект усугубляется при визуализации 3D-образцов, таких как клетки, содержащие области, заполненные жидкостью, которые рассеивают свет, что приводит к потере информации.
Конфокальная микроскопия
Конфокальная микроскопия совершенствует стандартную флуоресцентную микроскопию за счет использования точечных отверстий для отражения расфокусированного света (рис. 1), что приводит к более высокому разрешению, большей контрастности и уменьшению шума. Однако эта точечная диафрагма отображает только крошечную область образца (около 100 нм) и, следовательно, ее необходимо сканировать по всему образцу, что требует времени и может привести к повреждению фотографии. Этот формат известен как лазерная сканирующая конфокальная микроскопия (LSCM).
Рисунок 1: Использование точечного отверстия для блокировки нерезкого света. Свет сверху (а) или ниже (б) фокальной плоскости отклоняется отверстием, а свет из фокальной плоскости (в) проходит через отверстие к детектору.Изображение получено из Leica Science Lab.
Конфокальная микроскопия с вращающимся диском
Конфокальная микроскопия с вращающимся диском (SDCM) представляет собой альтернативу LSCM. Вместо одного отверстия в SDCM имеются сотни отверстий, расположенных по спирали на непрозрачном диске (рис. 2), который вращается с высокой скоростью. При вращении отверстия сканируют образец рядами, создавая изображение. Использование вращающегося диска значительно повышает скорость получения изображений (позволяя отображать быстрые динамические процессы и живые образцы) и значительно снижает повреждение фотографий.
Вместо одного отверстия в SDCM имеются сотни отверстий, расположенных по спирали на непрозрачном диске (рис. 2), который вращается с высокой скоростью. При вращении отверстия сканируют образец рядами, создавая изображение. Использование вращающегося диска значительно повышает скорость получения изображений (позволяя отображать быстрые динамические процессы и живые образцы) и значительно снижает повреждение фотографий.
отверстия в диске расположены так, что каждая часть изображения сканируется как
диск крутится. Изменяя скорость вращения диска, диаметр пинхола и/или
расстояние между отверстиями; яркость, контрастность и качество изображения могут быть оптимизированы,
делая SDCM гибко настраиваемыми. Однако при больших диаметрах отверстий
приводит к улучшению пропускания света через диск, а также снижает
разрешение, а большое расстояние между отверстиями устраняет любые отверстия
перекрестные помехи, это также снижает светопропускание.
Однако при больших диаметрах отверстий
приводит к улучшению пропускания света через диск, а также снижает
разрешение, а большое расстояние между отверстиями устраняет любые отверстия
перекрестные помехи, это также снижает светопропускание.
Наличие маленьких точечных отверстий с большим расстоянием между ними приведет к более высокому разрешению, но к самому низкому коэффициенту пропускания света через диск. Пропускание можно улучшить, добавив второй диск, который содержит линзы микрометрового масштаба вместо точечных отверстий. Диск с микролинзами фокусирует свет через каждое отверстие первичного диска, что значительно улучшает пропускание света к образцу, как показано на рисунке 3.
Рисунок 3: Использование вторичного диска с микролинзами для улучшения пропускания света через первичный дырочный диск. Лазерное излучение фокусируется микролинзами через точечные отверстия, при этом оба диска синхронно вращаются над образцом.Изображение получено от Graf et al.
 2005.
2005.Камеры для конфокальных микроскопов с вращающимся диском
Важным моментом, который следует учитывать, является то, что SDCM возбуждают/отображают несколько точек одновременно и могут вращаться с очень высокой скоростью, а это означает, что для захвата изображений с пример. Эти камеры должны иметь высокую частоту кадров из-за скорости вращающегося диска, поскольку более длительное время экспозиции или низкая скорость вращения диска могут привести к появлению полос на изображении. При использовании камер, способных работать с высокой скоростью вращения, получаются высококачественные изображения, как показано на рис. 4.
Изображение получено от Stehbens et al.
 2012.
2012.Резюме
Предложения SDCM явное улучшение по сравнению с LSCM и обычной флуоресцентной микроскопией, что позволяет для быстрой и эффективной визуализации живых образцов, динамических процессов и оптических разделение 3D-образцов на 2D-срезы. Многоканальные изображения могут быть получены в несколько длин волн, что приводит к высококачественным изображениям, насыщенным информацией, и существуют методы деконволюции для дальнейшего улучшения контрастности и качества изображения.
Основным недостатком СДКМ является то, что через диск к образцу передается только небольшая часть света, но с помощью настраиваемых дисков с точечными отверстиями, дисков с вторичными микролинзами и высокочувствительных камер эти ограничения можно легко преодолеть, а также улучшить визуализацию. скорость и поле зрения еще больше, чтобы создавать изображения с высоким разрешением быстрее, чем когда-либо.
Лаборатория реактивного движения Наука: Карл Штапельфельдт
Наука Лаборатории реактивного движения: Карл Штапельфельдт Пропустить навигациюПоиск людей:
Поиск проектов:
Поиск людей:
Поиск проектов:
Адрес:
4800 Oak Grove Drive
M/S 321-161
Пасадена, Калифорния
Виды учебной программы:
Нажмите здесь
Веб -сайт:
Нажмите здесь
Член:
Астрофизика и космические науки
Образование

Профессиональный опыт
- Лаборатория реактивного движения – Секция 9 астрофизики и космических наук6226
- Старший научный сотрудник (с 2021 г. по настоящее время)
- Главный научный сотрудник Программы исследования экзопланет НАСА (с 2016 г. по настоящее время)
- Главный научный сотрудник (2005–2011 гг.)
- Научный сотрудник (2000–2005 гг.) 4 Ученый (200995
- 4)
- Постдокторский научный сотрудник (1993-1994)
- Начальник лаборатории экзопланет и звездной астрофизики (2011-2016)
- Постдокторский научный сотрудник (1990–1993)
Научные интересы
- Астрофизика: миллиметровые наблюдения; коронография; моделирование рассеянного света и спектрального распределения энергии околозвездных дисков
- Миссии: Космический телескоп Хаббла Научная группа WFPC2, Научное бюро проекта космического телескопа Спитцер, Космическая обсерватория Гершеля, Ключевая научная группа LBTI Exozodi
- Миссионерские исследования: HabEx, LUVOIR, Exo-C (кафедра исследований), WFIRST, ACCESS, ATLAST, Terrestrial Planet Finder Coronagraph (исполняющий обязанности/заместитель научного сотрудника проекта), Eclipse
- AAAS Newcomb Cleveland Award (2009)
Избранные публикации
- Stapelfeldt, K.
 , Rauer, H., Roberge, A., and Mandel 2021 «Космические миссии для изучения экзопланет», глава 9в ЭКЗОГРАНИЦАХ: БОЛЬШИЕ ВОПРОСЫ ЭКЗОПЛАНЕТАРНОЙ НАУКИ (глава с приглашенным обзором), под ред. Н. Мадхусудхана. IOP Press, в печати
, Rauer, H., Roberge, A., and Mandel 2021 «Космические миссии для изучения экзопланет», глава 9в ЭКЗОГРАНИЦАХ: БОЛЬШИЕ ВОПРОСЫ ЭКЗОПЛАНЕТАРНОЙ НАУКИ (глава с приглашенным обзором), под ред. Н. Мадхусудхана. IOP Press, в печати - Villenave, M., Ménard, F., Dent, W. R. F., Duchêne, G., Stapelfeldt, K. R. et al. 2020 «Наблюдения протопланетных дисков с ребра с помощью ALMA. I. Результаты по континуальным данным» A.&A. 642 A164
- Фарамаз, В., Крист, Дж.Э., Штапельфельдт, К.Р. и др. 2019 «От рассеянного света к миллиметровому излучению: всесторонний взгляд на систему HD 202628 гигалетней давности и ее эксцентричное кольцо обломков» А.Дж. 158 162
- Robinson, T., Stapelfeldt, K., Marley, M (2016) «Характеристика каменистых и газообразных экзопланет с помощью космических коронографов 2-метрового класса: общие соображения» P.A.S.P. 128 5003
- Stapelfeldt, K. et al. (2015) Заключительный отчет об исследовании миссии Exo-C, Внутренний документ Программы исследования экзопланет НАСА по адресу https://exoplanets.
 nasa.gov/exep/studies/probe-scale-stdt/
nasa.gov/exep/studies/probe-scale-stdt/ - Krist, J., Stapelfeldt, К., Брайден Г. и Плавчан П. (2012) «Наблюдения космического телескопа Хаббла за диском обломков HD 202628», А.Дж. 144 45
- Su, K.Y.L, Rieke, G.H, Stapelfeldt, K.R. и др. (2009) «Диск мусора вокруг HR 8799», Ap.J. 678 985
- Калас, П. и др. (2008) «Оптические изображения экзосолнечной планеты в 25 световых годах от Земли» Science 322 1345
- Rebull, LM, Stapelfeldt, K.R. и др. (2008) «Наблюдения Spitzer/MIPS звезд в движущейся группе бета Живописца» Ap.J. 681 1484
- Уотсон, А. М., Stapelfeldt, K.R., Wood, K., and Menard, F. (2007) «Многоволновое изображение дисков молодых звездных объектов: к пониманию структуры диска и эволюции пыли», в PROTOSTARS AND PLANETS V., B. Reipurth, Д. Джуитт и К. Киль, ред., Univ. Arizona Press, Tucson, стр. 523-538.
- Штапельфельдт, К.Р. и др. (2004) «Первый взгляд на диск мусора Фомальгаута с помощью космического телескопа Спитцер», Ap.
 J.Suppl. 154 458
J.Suppl. 154 458 - Штапельфельдт, К.Р. и др. (2003) «Космический телескоп Хаббл WFPC2, изображение диска и струи HV Tauri C», Ap.J. 589 410
- Крист, Дж., Стапельфельдт, К. и др. (2000) «Изображения WFPC2 диска, окружающего TW Hydrae», Ap.J. 538 793.
- Маккориан, М., Стапельфельдт, К., и Клоуз, Л. (2000) «Оптическое и ближнее инфракрасное изображение молодых околозвездных дисков с высоким разрешением», обзорная статья в PROTOSTARS AND PLANETS IV, V , Мэннингс, А. Босс и С. Рассел, ред., 9.0273 Унив. Arizona Press, Tucson, p. 485
- Паджетт Д.Л., Бранднер В., Стапельфельдт К.Р. и др. (1999) «Визуализация дисков и оболочек вокруг очень молодых звезд HST/NICMOS» AJ 117 1490
- Stapelfeldt, KR и др. (1998) «Околозвездный диск с ребра в молодой двойной системе HK Tauri» , Ап.Дж. 502 L65
- Burrows, C.J., Stapelfeldt, K.R. и др. (1996) «HST-изображение диска и струи HH 30», Ап.
 Дж. 473 437
Дж. 473 437 - Штапельфельдт, К.Р. и др. (1995) «Визуализация WFPC2 околозвездной туманности HL Тельца», Ap.J. 449 888
- Stapelfeldt, KR и др. (1991) «Узкополосные изображения трех объектов Хербига-Аро в ближнем инфракрасном диапазоне», Ап.Дж. 371 226
Qu’est-ce qu’ODX (выгруженная передача данных хранилища Windows) ?
Par Thomas Rothschilds
Комментарий к клиенту, продолжающемуся с выступлениями, а также предоставленному ранее стандарту для сравнения ЧТЕНИЕ/ЗАПИСЬ в ODX — и комментарии к инженерным разработкам и частям метрик Qumulo Core, к циклу быстрой публикации et de l’expérience de mise à niveau Transparente pour découvrir et résoudre le mystère !
Qu’est-ce qu’ODX (Передача выгруженных данных хранилища Windows) ? Windows Storage Offloaded Data Transfer (ODX) fait partie du protocole SMB (Server Message Block) où vous pouvez dire au système de fichiers Qumulo de copier un morceau d’un fichier d’un fichier à un autre sans envoyer les données via ла машинный клиент. ODX améliore les performances de copie un peu comme la copie côté serverur (SSC). Il élimine la la lance du réseau entre le client et le serveur et permet à Qumulo Core d’optimiser la taille et la mise en mémoire tampon des E/S. Сравнивая ODX с SSC, нет результатов внутренних тестов, установленных для ODX 7 fois plus rapide et SSC 4 fois plus quicke que la séquence READ/WRITE typeique qui se produit lors de la copie d’un fichier vers un autre emplacement sur le мем обслуживающий персонал.
ODX améliore les performances de copie un peu comme la copie côté serverur (SSC). Il élimine la la lance du réseau entre le client et le serveur et permet à Qumulo Core d’optimiser la taille et la mise en mémoire tampon des E/S. Сравнивая ODX с SSC, нет результатов внутренних тестов, установленных для ODX 7 fois plus rapide et SSC 4 fois plus quicke que la séquence READ/WRITE typeique qui se produit lors de la copie d’un fichier vers un autre emplacement sur le мем обслуживающий персонал.
En 2021, nous avons Fourni Le Support ODX for Qumulo Core версии 3.0.0 или выше. Peu de temps après l’expédition, un client a signalé que les performances d’ODX étaient plus lentes que prévu.
Sachant qu’ODX lit à partir d’un fichier et écrit dans un autre, nous avons d’abord supçonné que les performances d’écriture étaient le problème. En règle générale, les opérations de lection prennent au max quelques миллисекунды (merci Mise en cache et prélecture SSD!). Pourtant, lorsque nous avons, наблюдая за задержкой лекции, nous avons vu qu’il s’agissait d’une plus grande partie de la lance ODX, que ce à quoi nous nous Attensions — de l’ordre de 25 ms (окружающая среда), avec des pics plus élevés на 40 или 50 мс. Qu’est-ce qui se passe avec ca? Голоса за визуализацию продолжительности жизни фазы фазы лекции операции ODX :
Pourtant, lorsque nous avons, наблюдая за задержкой лекции, nous avons vu qu’il s’agissait d’une plus grande partie de la lance ODX, que ce à quoi nous nous Attensions — de l’ordre de 25 ms (окружающая среда), avec des pics plus élevés на 40 или 50 мс. Qu’est-ce qui se passe avec ca? Голоса за визуализацию продолжительности жизни фазы фазы лекции операции ODX :
Рисунок 1 : Длительность запроса ODX – Lire
Мы постоянно изучаем данные о представлениях серии временных периодов, чтобы получить точные данные о сборах через отдельный конвейер облака наблюдения. En moyenne, notre taux de réussite du cache RAM et nos mesures de latence semblaient bonnes. Больше внимания уделяете специальным лекциям на ODX étaient-elles généralement lentes ?
Le premier indice Au fur et à mesure que nous nous rapprochions de la découverte de la case première, nous avions besoin de mesures de granularité plus élevées spécifiques à une seule Cluster de Travail le ODX suransce другие операции. Heureusement, nous avons un outil, appelé 9Триггер 6531, созданный нами внутри компании, который при необходимости собирает такие распределенные данные о производительности. Мы работали с нашим клиентом над профилированием некоторых конкретных последовательностей ODX и использовали триггер
Heureusement, nous avons un outil, appelé 9Триггер 6531, созданный нами внутри компании, который при необходимости собирает такие распределенные данные о производительности. Мы работали с нашим клиентом над профилированием некоторых конкретных последовательностей ODX и использовали триггер для сбора данных во время этих последовательностей. Мы узнали пару вещей. (См. Рисунок 1 выше.)
В каждой операции чтения большинство блоков находились в кэше ОЗУ, но при каждом чтении отсутствовал кэш для нескольких блоков. Когда это происходит, транзакция файловой системы должна считывать данные с самих устройств хранения. В этом случае метрики сказали нам, что данные находятся на вращающихся дисках. Примечание: Про себя я подумал: «Конечно, это должны были быть вращающиеся диски… это ВСЕГДА вращающиеся диски». Я должен был знать, что поиски — это единственное, что может увеличить задержку до 50 мс. Вращающиеся диски могут эффективно передавать данные, когда запросы ставятся в очередь в непрерывном порядке; начиная с начала файла и читая до конца. Однако в этом случае мы пропускали только несколько блоков из кеша на операцию чтения ODX, что проявляется на вращающемся диске как множество несмежных операций чтения. Это плохая новость для задержки вращающегося диска. Обычно операции чтения файловой системы не вызывают такой задержки с вращающимся диском, потому что у нас есть эффективный префетчер. Префетчер угадывает, что будет считано дальше, и заранее загружает это в кеш. У префетчера есть шаблон ввода-вывода, оптимизированный для чтения с вращающихся дисков. Итак, почему не работал префетчер? У нашего модуля предварительной выборки есть метрики, описывающие, насколько он успешен в среднем. Мы проверили журналы операций, чтобы увидеть шаблон ввода-вывода. Журналы операций — это инструмент для текстовых файлов журналов, который сообщает нам информацию о каждой операции, такую как смещение, размер и попадание или промах кеша. Однако мы не ожидали, что нам потребуются размеры чтения ODX и смещения в наших журналах операций, и в результате этот код не был подключен! Поэтому нам пришлось написать еще немного кода и дождаться обновления… Рисунок 2 : Как должна работать предварительная выборка Рисунок 3 : Как должна работать предварительная выборка (после второго чтения) Рисунок 4 : Как должна работать предварительная выборка (после третьего чтения) Рисунок 5 : Как должна работать предварительная выборка Через пару недель мы отправили новый код, и с помощью наших замечательных обновлений клиент вскоре смог обновить свою систему хранения Qumulo до последней версии. Помню, сначала мои глаза остекленели… я что, неправильно прочитал цифры? Как в каждом запросе отсутствует кеш только для 256 КБ из 8 МБ, которые он запрашивал? Как предварительная выборка извлекает только подмножество каждого запроса? Это невозможно! Примечание: Первая стадия любой ошибки — это отрицание — убеждение, что данные неверны. К счастью, это было не первое мое родео. Я быстро подавил свое отрицание и начал спрашивать себя: «Как такое возможно?» Я начал объяснять, как работает программа предварительной выборки, своему коллеге, который работал со мной над расследованием. Иллюстрация 1 : Проблема предварительной выборки (первое чтение файла) Иллюстрация 2 : Проблема предварительной выборки (после второго чтения) Иллюстрация 3 : Проблема предварительной выборки (после третьего чтения) Рисунок 4 : Размер ввода-вывода чтения с предварительной выборкой больше, чем размер ввода-вывода с предварительной выборкой Рисунок 5 : Проблема предварительной выборки (после четвертого чтения) Выявление ошибки — это только начало. В голову сразу пришло три вопроса: Наш планировщик протоколов файловой системы обрабатывает все запросы протоколов. Типичный размер запроса протокола составляет 1 МБ. Когда мы получаем запросы на чтение протокола, мы обрабатываем их и, возможно, объединяем запросы для оптимизации производительности чтения. Естественно, у нас есть максимальный комбинированный размер ввода-вывода для этих запросов к файловой системе. Если вы позволите размеру ввода-вывода стать слишком большим, то запрос может быть узким местом в какой-то большой однопоточной задаче, которую он выполнял (например, ЦП, выделение памяти). Таким образом, наш планировщик файловой системы делает максимальный комбинированный запрос на чтение 8 МБ, такой же, как и максимальный размер ввода-вывода нашего префетчера. Это было задумано. Таким образом, в этих рабочих нагрузках модуль предварительной выборки выполняет предварительную выборку всего, хотя он никогда не опережает более чем на 8 МБ, если общий размер операций ввода-вывода также составляет 8 МБ… ( царапает голову … что тоже не было предусмотрено поведением …). Сама операция ODX проходит через планировщик, но не передает свой внутренний запрос на чтение через планировщик. Затем ODX устанавливал максимальный размер чтения ввода-вывода, который он запрашивал, независимо от планировщика. Мы обнаружили, что максимальный размер ввода-вывода планировщика и максимальный размер ввода-вывода ODX используют разные функции: Планировщик использовал Итак, это была наша первопричина. Мы исправили код протокола ODX для использования Наши тесты производительности ODX сделали , фактически, демонстрируют поведение некэшированных хвостов. Но выступление было не таким уж плохим; потому что в этом тесте производительности данные были достаточно малы, чтобы поместиться в кэш SSD! Оглядываясь назад на Рисунок 1 (выше), вы можете видеть, что задержка чтения с SSD намного ниже, чем у вращающегося диска. Таким образом, из первых результатов тестов производительности было не так очевидно, что префетчер делает что-то не так. Тест не проверял метрики префетчера явно. После того, как мы изменили тест производительности, чтобы сделать второй шаг удаления данных с SSD, а затем прочитать их обратно с вращающегося диска, общая производительность была значительно хуже, чем должна была быть, что выявило ошибку. Мы исправили ошибку, наблюдали за улучшением этого автоматизированного теста производительности и отправили улучшение через 2 недели. Неструктурированные данные повсюду, и их количество растет неконтролируемыми темпами. ИТ-директора и ИТ-руководители обращаются к масштабируемым решениям для хранения данных, чтобы управлять этими данными и оставаться конкурентоспособными. Блочное хранилище, хранилище объектов и хранилище файлов имеют уникальные возможности и ограничения, а это означает, что системы хранения корпоративного уровня не являются универсальными решениями.  С крутящимися дисками у меня не самые лучшие отношения. У них есть раздражающая, но полезная привычка мучительно выявлять непреднамеренное поведение в чувствительных к производительности путях кода.
С крутящимися дисками у меня не самые лучшие отношения. У них есть раздражающая, но полезная привычка мучительно выявлять непреднамеренное поведение в чувствительных к производительности путях кода. Эти метрики сказали нам, что все, что было предварительно загружено, читалось, но некоторые данные, прочитанные файловой системой, не были предварительно загружены… это действительно странно! Может быть, операции ODX считываются не по порядку или прыгают случайным образом? Предварительная выборка плохо справляется со случайным вводом-выводом.
Эти метрики сказали нам, что все, что было предварительно загружено, читалось, но некоторые данные, прочитанные файловой системой, не были предварительно загружены… это действительно странно! Может быть, операции ODX считываются не по порядку или прыгают случайным образом? Предварительная выборка плохо справляется со случайным вводом-выводом. Как работает предварительная выборка (примеры иллюстраций)
 Они повторно запустили тестовую нагрузку для нас. Используя улучшенную регистрацию операций, мы нашли еще одну загадку! Читая журналы операций (я чувствовал, что нахожусь в матрице, читая зеленые числа), мы обнаружили, что наш код протокола ODX отправлял в файловую систему непрерывные запросы на чтение по 8650752 байта каждый. Когда мы сделали математику, получилось 8 мегабайт + 256 КБ. Но! Журнал операций показал, что каждый запрос ODX на самом деле получал только 8388608 байт из кеша (ровно 8 мегабайт).
Они повторно запустили тестовую нагрузку для нас. Используя улучшенную регистрацию операций, мы нашли еще одну загадку! Читая журналы операций (я чувствовал, что нахожусь в матрице, читая зеленые числа), мы обнаружили, что наш код протокола ODX отправлял в файловую систему непрерывные запросы на чтение по 8650752 байта каждый. Когда мы сделали математику, получилось 8 мегабайт + 256 КБ. Но! Журнал операций показал, что каждый запрос ODX на самом деле получал только 8388608 байт из кеша (ровно 8 мегабайт). Предварительная выборка должна опережать рабочую нагрузку чтения, чтобы размер операций ввода-вывода рабочей нагрузки чтения не имел значения. Предварительная выборка всегда извлекает данные большими порциями и таким образом, чтобы очередь на вращающихся дисках была упорядочена, чтобы избежать операций поиска. И тут меня осенило… больших фрагмента … насколько велики фрагменты предварительной выборки? OH ... они 8 МБ ... подождите, это жутко. И как он опережает рабочую нагрузку по чтению? OH , мы запускаем одну предварительную выборку на каждый запрос на чтение… подождите… соединяем эти две вещи вместе… если мы запускаем только одну предварительную выборку на запрос на чтение, а размер фрагмента предварительной выборки составляет не более 8 МБ, а устройство чтения читает фрагменты из 8 МБ + 256 КБ… тогда да, очевидно, префетчер никогда не продвинется вперед… он всегда будет выполнять предварительную выборку следующих 8 МБ, оставляя хвост в 256 КБ некэшированным.
Предварительная выборка должна опережать рабочую нагрузку чтения, чтобы размер операций ввода-вывода рабочей нагрузки чтения не имел значения. Предварительная выборка всегда извлекает данные большими порциями и таким образом, чтобы очередь на вращающихся дисках была упорядочена, чтобы избежать операций поиска. И тут меня осенило… больших фрагмента … насколько велики фрагменты предварительной выборки? OH ... они 8 МБ ... подождите, это жутко. И как он опережает рабочую нагрузку по чтению? OH , мы запускаем одну предварительную выборку на каждый запрос на чтение… подождите… соединяем эти две вещи вместе… если мы запускаем только одну предварительную выборку на запрос на чтение, а размер фрагмента предварительной выборки составляет не более 8 МБ, а устройство чтения читает фрагменты из 8 МБ + 256 КБ… тогда да, очевидно, префетчер никогда не продвинется вперед… он всегда будет выполнять предварительную выборку следующих 8 МБ, оставляя хвост в 256 КБ некэшированным. ВАУ . (Ручной насос). Ok. Мы нашли дымящийся пистолет.
ВАУ . (Ручной насос). Ok. Мы нашли дымящийся пистолет. Пример иллюстрации проблемы предварительной выборки
1.
 Почему эта проблема не возникает в наших стандартных тестах производительности чтения файловой системы?
Почему эта проблема не возникает в наших стандартных тестах производительности чтения файловой системы?
2. Почему ODX использует размер ввода-вывода 8 МБ + 256 КБ?
fs_target_transaction_size()
fs_max_transaction_size() fs_target_transaction_size, что составляет минимум fs_max_transaction_size и 8 МБ! Принимая во внимание, что код ODX интуитивно использовал fs_max_transaction_size, который вычисляется и оказывается равным 8 МБ + 256 КБ. fs_target_transaction_size и voilà , больше не кешированные хвосты для запросов на чтение.
3. Почему наши тесты производительности ODX не выявили этого?
 Еще раз воспользовавшись простыми обновлениями Qumulo, наши клиенты смогли выполнить обновление вскоре после исправления и получить улучшенную производительность ODX.
Еще раз воспользовавшись простыми обновлениями Qumulo, наши клиенты смогли выполнить обновление вскоре после исправления и получить улучшенную производительность ODX. Новый учебник по хранению корпоративных данных


 Запишите значение как «В».
Запишите значение как «В». 06.2008, 22:10
#1
06.2008, 22:10
#1
 5 на J6.5 какой вылет должен быть у новых дискав, что бы они не терлись об внутренности подвески? поиграв с вылетом моего будущего колеса получаем значение — 32 мм, т.е. был вылет 45 а нужен теперь 32.
5 на J6.5 какой вылет должен быть у новых дискав, что бы они не терлись об внутренности подвески? поиграв с вылетом моего будущего колеса получаем значение — 32 мм, т.е. был вылет 45 а нужен теперь 32.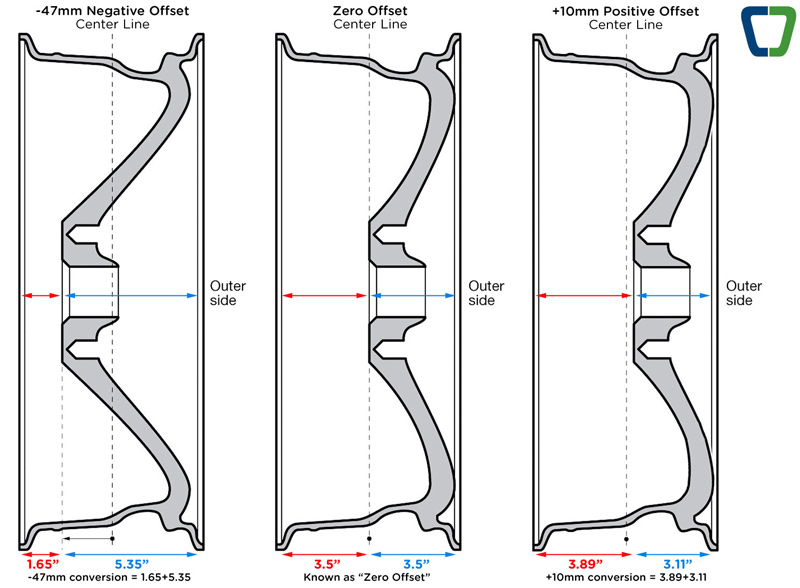 5 на 6.5 одного диаметра или же будет переход на больший?
5 на 6.5 одного диаметра или же будет переход на больший?
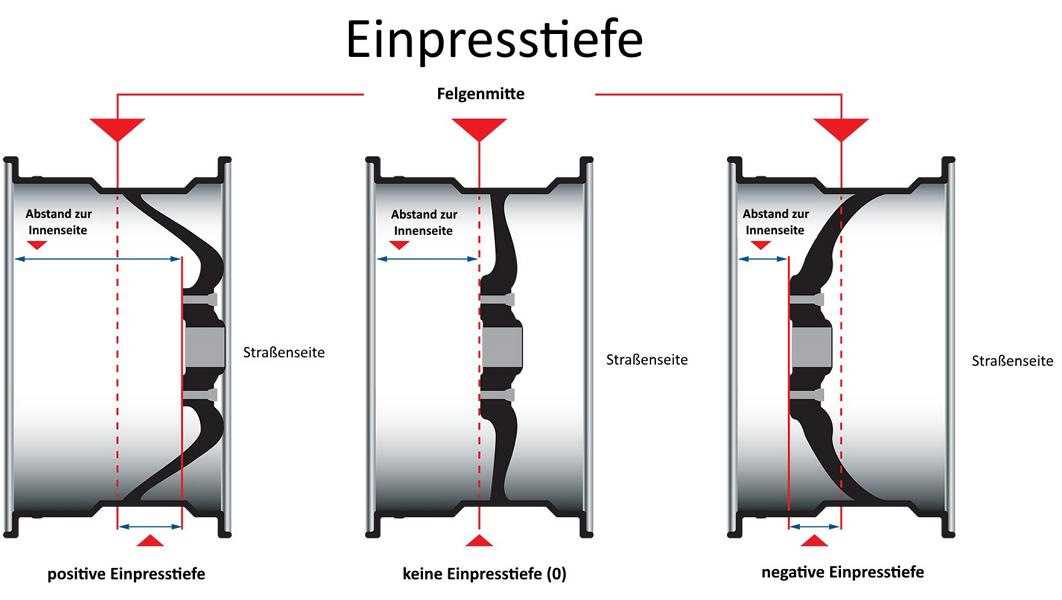 Вылет может быть нулевым, положительным (ступица диска выпячена наружу относительно середины обода) и отрицательным (ступица утоплена).
Вылет может быть нулевым, положительным (ступица диска выпячена наружу относительно середины обода) и отрицательным (ступица утоплена). 5J R15 ET=43 (до 40) встанет без проблем.
5J R15 ET=43 (до 40) встанет без проблем.
 …….все равно будет очень приблизительно. Покрышка шириной 195 оптимальна садиться на диск шириной 6.5J, я ставил и на родную 6J-все без проблем. Могу даже почти на 100% сказать что при ширине покрышки 195 и диска 6Jx15 все встанет без проблем на ЕТ=45. Почему «почти», так как ставил на р11,но если не изменяет память на р10 все тоже самое.
…….все равно будет очень приблизительно. Покрышка шириной 195 оптимальна садиться на диск шириной 6.5J, я ставил и на родную 6J-все без проблем. Могу даже почти на 100% сказать что при ширине покрышки 195 и диска 6Jx15 все встанет без проблем на ЕТ=45. Почему «почти», так как ставил на р11,но если не изменяет память на р10 все тоже самое.

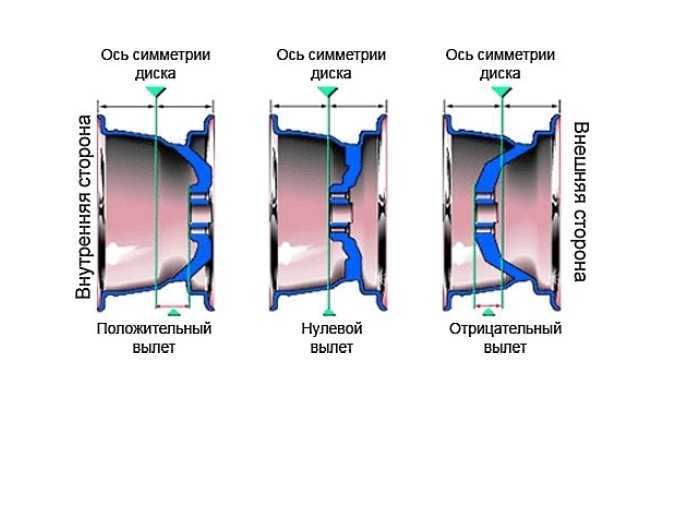 primera-club.ru/forum/board/21.htm
primera-club.ru/forum/board/21.htm
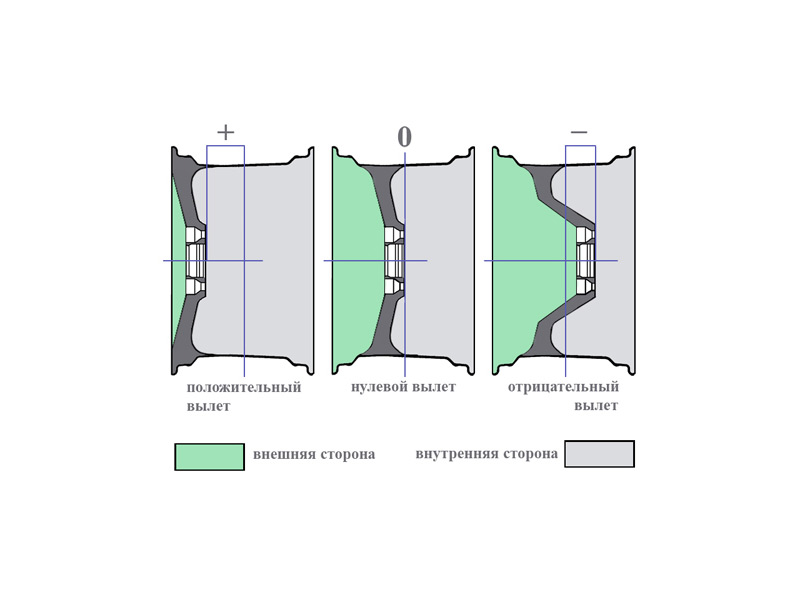 ..
.. 6
6